题目内容
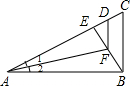 如图,AB⊥BC于B,BE⊥AC于E,∠1=∠2,D为AC上一点,AD=AB,则
如图,AB⊥BC于B,BE⊥AC于E,∠1=∠2,D为AC上一点,AD=AB,则
- A.∠1=∠EFD
- B.FD∥BC
- C.BF=DF=CD
- D.BE=EC
B
分析:由SAS易证△ADF≌△ABF,根据全等三角形的对应边相等得出∠ADF=∠ABF,又由同角的余角相等得出∠ABF=∠C,则∠ADF=∠C,根据同位角相等,两直线平行,得出FD∥BC.
解答:在△ADF与△ABF中,
∵AF=AF,∠1=∠2,AD=AB,
∴△ADF≌△ABF,
∴∠ADF=∠ABF,
又∵∠ABF=∠C=90°-∠CBF,
∴∠ADF=∠C,
∴FD∥BC.
故选B.
点评:本题考查了平行线的判定,余角的性质,全等三角形的判定与性质,属于基础题型,难度中等.
分析:由SAS易证△ADF≌△ABF,根据全等三角形的对应边相等得出∠ADF=∠ABF,又由同角的余角相等得出∠ABF=∠C,则∠ADF=∠C,根据同位角相等,两直线平行,得出FD∥BC.
解答:在△ADF与△ABF中,
∵AF=AF,∠1=∠2,AD=AB,
∴△ADF≌△ABF,
∴∠ADF=∠ABF,
又∵∠ABF=∠C=90°-∠CBF,
∴∠ADF=∠C,
∴FD∥BC.
故选B.
点评:本题考查了平行线的判定,余角的性质,全等三角形的判定与性质,属于基础题型,难度中等.

练习册系列答案
相关题目
 11、如图,AB⊥BC于B,AD⊥CD于D,若CB=CD,且∠BAC=30°,则∠BAD的度数是( )
11、如图,AB⊥BC于B,AD⊥CD于D,若CB=CD,且∠BAC=30°,则∠BAD的度数是( )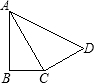 如图,AB⊥BC于B,AC⊥CD于C,添加一个条件:
如图,AB⊥BC于B,AC⊥CD于C,添加一个条件:
 如图,AB⊥BC于B,AC⊥CD于C,添加一个条件:
如图,AB⊥BC于B,AC⊥CD于C,添加一个条件: 如图,AB⊥BC于B,AE⊥BE于E,AB∥DC,若AB=BD=6,DE-DC=1,则DE的长为
如图,AB⊥BC于B,AE⊥BE于E,AB∥DC,若AB=BD=6,DE-DC=1,则DE的长为