题目内容
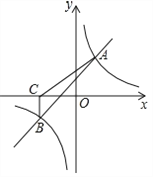
【题目】如图直线L与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0).
(1)请求出直线L的函数解析式;
(2)点P在坐标轴上,且△ABP的面积为12,求点P的坐标;
(3)点C为直线AB上一个动点,是否存在使点C到x轴的距离为1.5若存在请直接写出该点的坐标.
【答案】(1)y=0.75x+3;(2)点P的坐标为(4,0)或(-12,0)或(0,3)或(0,9);(3)存在点C到x轴的距离为1.5,其坐标是(-2,1.5)或(-6,-1.5).
【解析】
(1)设直线L的解析式为y=kx+b(k≠0),把A,B代入求解即可;
(2)根据S△ABP的面积为12,分成①当P点在x轴上时,②当P点在y轴上时,两种情况讨论即可;
(3)假设存在点C(x,±1.5)到x轴的距离为1.5,将点C代入直线L的解析式求解判断即可.
解:(1)设直线L的解析式为y=kx+b(k≠0),
把A(0,3),B(-4,0)代入得![]() ,
,
解得![]() ,
,
∴解析式为:y=0.75x+3;
(2)∵A(0,3),B(-4,0),
∴|OA|=3,|OB|=4,
①当P点在x轴上时S△ABP=![]() ·|OB|·|AP|=
·|OB|·|AP|=![]() ×3·|AP|=12,
×3·|AP|=12,
解得:|AP|=8,
∴可得点P的坐标为:(4,0)或(-12,0),
②当P点在y轴上时S△ABP=![]() ·|OA|·|BP|=
·|OA|·|BP|=![]() ×4·|BP|=12,
×4·|BP|=12,
解得:|BP|=6,
∴可得点P的坐标为:(0,3)或(0,9),
综上:点P的坐标为(4,0)或(-12,0)或(0,3)或(0,9);
(3)假设存在点C(x,±1.5)到x轴的距离为1.5,则点C(x,±1.5)满足方程y=0.75x+3,
①当C(x,1.5)时,1.5=0.75x+3,
解得x=-2,
∴点C(-2,1.5)存在,
②当C(x,-1.5)时,-1.5=0.75x+3,
解得x=-6,
∴C(-6,-1.5)存在,
∴存在点C到x轴的距离为1.5,其坐标是(-2,1.5)或(-6,-1.5).

 名校课堂系列答案
名校课堂系列答案