Question

【题目】在平面直角坐标系中，已知，，且，的面积为3.

（1）直接写出 ， ， .

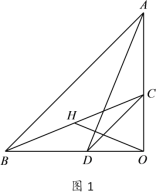
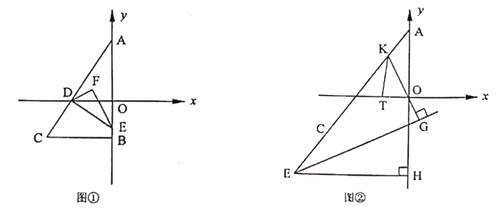
（2）如图①，设交轴于，交轴于点，、的角平分线交于点，求的大小.

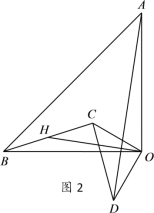
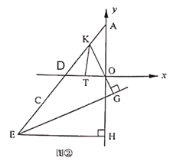
（3）如图②，点是延长线上动点，轴于点，平分，直线于，交于点，平分交轴于点，求的值.

Answer 1

【答案】（1），，；（2）；（3）的值是.

【解析】

（1）根据算术平方根和绝对值的非负性求出a、b的值，再利用三角形的面积公式求出m的值即可；

（2）首先证明∠ADO＝∠AED，根据三角形的内角和定理和角平分线的定义，即可解决问题；

（3）如图②中，先根据三角形外角的性质得：∠KTO＝∠KDO＋∠DKT，然后结合角平分线的性质可得：2∠KTO3∠GEH＝∠GEH＋∠EKG，最后由直角三角形的两锐角互余可得结论．

解：（1）（1）∵，

∴a2＝0，（b＋1）2＝0，

∴a＝2，b＝1，

∵△ABC的面积为3，

∴S△ABC＝ABBC＝3，

即×(m)×(2＋1)＝3，m＝2，

故答案为：2，1，2；

（2）依题意有和都是直角三角形

∴

∴

∴

（3）设交轴于点，依题意有：轴，

∴，

∴，

∴，

∴所求的值是.