题目内容
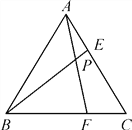
【题目】如图,在△ABC中,AB=AC=10cm,BC=16cm,DE=4cm.动线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时运动停止.过点E作EF∥AC交AB于点F(当点E与点C重合时,EF与CA重合),连接DF,设运动的时间为t秒(t≥0).
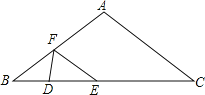
(1)直接写出用含t的代数式表示线段BE、EF的长;
(2)在这个运动过程中,△DEF能否为等腰三角形?若能,请求出t的值;若不能,请说明理由;
(3)设M、N分别是DF、EF的中点,求整个运动过程中,MN所扫过的面积.
【答案】(1)BE=(t+4)cm;EF=![]() (t+4)cm;(2)当t=0、
(t+4)cm;(2)当t=0、![]() 或
或![]() 秒时,△DEF为等腰三角形;(3)整个运动过程中,MN所扫过的面积为
秒时,△DEF为等腰三角形;(3)整个运动过程中,MN所扫过的面积为![]() cm2.
cm2.
【解析】
解:(1)![]() ,
,
![]() .
.
(2)分三种情况讨论:
①当![]() 时,
时,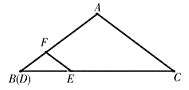
有![]()
∴点![]() 与点
与点![]() 重合,
重合,
∴![]()
②当![]() 时,
时,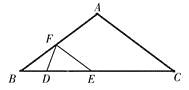
∴![]() ,
,
解得:![]()
③当![]() 时,
时,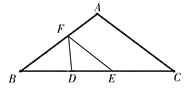
有![]()
∴△DEF∽△ABC.
∴![]() , 即
, 即![]() ,
,
解得:![]() .
.
综上所述,当![]() 、
、![]() 或
或![]() 秒时,△
秒时,△![]() 为等腰三角形.
为等腰三角形.
(3)设P是AC的中点,连接BP,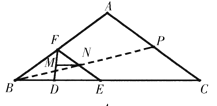
∵![]() ∥
∥![]()
∴△![]() ∽△
∽△![]() .
.
∴![]() ∴
∴![]()
又![]() ∴△
∴△![]() ∽△
∽△![]()
∴![]()
∴点![]() 沿直线BP运动,MN也随之平移.
沿直线BP运动,MN也随之平移.
如图,设MN从ST位置运动到PQ位置,则四边形PQST是平行四边形.
∵![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,∴
的中点,∴![]() ∥DE,且ST=MN=
∥DE,且ST=MN=![]()
分别过点T、P作TK⊥BC,垂足为K,PL⊥BC,垂足为L,延长ST交PL于点R,则四边形TKLR是矩形,
当t=0时,EF=![]() (0+4)=
(0+4)=![]() TK=
TK=![]() EF·
EF·![]() ·
·![]() ·
·![]()
当t=12时,EF=AC=10,PL=![]() AC·
AC·![]() ·10·
·10·![]()
∴PR=PL-RL=PL-TK=3-![]()
∴![]() ·PR=2×
·PR=2×![]()
∴整个运动过程中,MN所扫过的面积为![]() cm2. 13分
cm2. 13分
(1)由题意得![]() ,利用相似比求出EF的长
,利用相似比求出EF的长
(2)分三种情况讨论:①当![]() 时,②当
时,②当![]() 时, ③当
时, ③当![]() 时
时
(3)设P是AC的中点,连接BP,通过相似证得![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,求得ST="2" ,分别过点T、P作TK⊥BC,垂足为K,PL⊥BC,垂足为L,延长ST交PL于点R,则四边形TKLR是矩形,利用三角函数求得PL、TK的值,得出PR的值,从而得出结论
的中点,求得ST="2" ,分别过点T、P作TK⊥BC,垂足为K,PL⊥BC,垂足为L,延长ST交PL于点R,则四边形TKLR是矩形,利用三角函数求得PL、TK的值,得出PR的值,从而得出结论

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案