题目内容
【题目】小聪与同桌小明在课下学习中遇到这样一道数学题:“如图(1),在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试确定线段AE与DB的大小关系,并说明理由”.小敏与小颖讨论后,进行了如下解答: 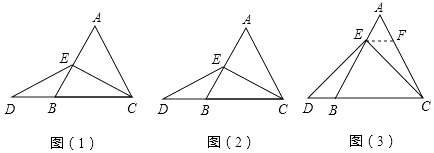
(1)取特殊情况,探索讨论: 当点E为AB的中点时,如图(2),确定线段AE与DB的大小关系,请你写出结论:AEDB(填“>”,“<”或“=”),并说明理由.
(2)特例启发,解答题目: 解:题目中,AE与DB的大小关系是:AEDB(填“>”,“<”或“=”).理由如下:如图(3),过点E作EF∥BC,交AC于点F.(请你将剩余的解答过程完成)
(3)拓展结论,设计新题: 在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,若△ABC的边长为1,AE=2,则CD的长为 . (请你画出图形,并直接写出结果).
【答案】
(1)=
(2)=
(3)3或1
【解析】解:(1.)AE=DB, 理由如下:∵ED=EC,
∴∠EDC=∠ECD,
∵三角形ABC是等边三角形,
∴∠ACB=∠ABC=60°,
∵点E为AB的中点,
∴∠ECD= ![]() ∠ACB=30°,
∠ACB=30°,
∴∠EDC=30°,
∴∠D=∠DEB=30°,
∴DB=BE,
∵AE=BE,
∴AE=DB,
所以答案是:=;
(2.)如图3,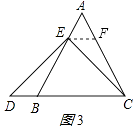
∵△ABC为等边三角形,且EF∥BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,∠FEC=∠ECB,
∴∠EFC=∠DBE=120°,
∵ED=EC,
∴∠D=∠ECB,∠D=∠FEC,
在△EFC与△DBE中,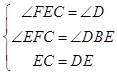 ,
,
∴△EFC≌△DBE(AAS),
∴EF=DB,
∵∠AEF=∠AFE=60°,
∴△AEF为等边三角形,
∴AE=EF,AE=BD,
所以答案是:=;
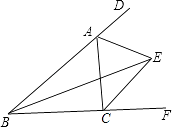
(3.)如图4,当点E在AB的延长线上时,过点E作EF∥BC,交AC的延长线于点F,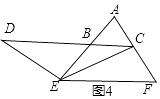
则∠DCE=∠CEF,∠DBE=∠AEF,∠ABC=∠AEF,∠ACB=∠AFE,
∵△ACB为等边三角形,
∴∠ABC=∠ACB=60°,
∴∠AEF=∠AFE=60°,∠DBE=∠ABC=60°,
∴∠DBE=∠EFC,而ED=EC,
∴∠D=∠DCE,∠D=∠CEF,
在△BDE与△FEC中,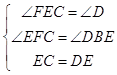 ,
,
∴△BDE≌△FEC(AAS),
∴BD=EF,
∵△AEF为等边三角形,
∴AE=EF=2,BD=EF=2,
∴CD=1+2=3;
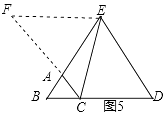
如图5,当点E在BA的延长线上时,过点E作EF∥BC,交CA的延长线于点F,
类似上述解法,同理可证:DB=EF=2,BC=1,
∴CD=2﹣1=1,
所以答案是:3或1.