题目内容
已知:抛物线y=x2-mx+| m2 |
| 2 |
| 3 |
| 4 |
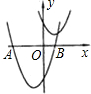 示,其中一条与x轴交于A、B两点.
示,其中一条与x轴交于A、B两点.(1)试判定哪条抛物线经过A、B两点,并说明理由;
(2)若A、B两点到原点的距离AO、OB满足
| 1 |
| OB |
| 1 |
| OA |
| 2 |
| 3 |
分析:(1)只需令每一条抛物线的解析式等于0,计算每一个方程的判别式△的值,使△>0的即为所求;
(2)如果设点A(x1,0),B(x2,0),则x1、x2是方程x2+mx-
m2=0的两个实数根,根据一元二次方程根与系数的关系及已知条件
-
=
,可求出m的值,进而得到抛物线的解析式.
(2)如果设点A(x1,0),B(x2,0),则x1、x2是方程x2+mx-
| 3 |
| 4 |
| 1 |
| OB |
| 1 |
| OA |
| 2 |
| 3 |
解答:解:(1)∵抛物线不过原点,
∴m≠0.
令x2-mx+
=0,
∴△1=(-m)2-4×
=-m2<0,与x轴没有交点.
令x2+mx-
m2=0,
∵△2=m2-4(-
m2)=4m2>0,
∴抛物线y=x2+mx-
m2经过A、B两点;
(2)设点A(x1,0),B(x2,0),
则x1、x2是方程x2+mx-
m2=0的两个实数根,
∴x1+x2=-m,x1•x2=-
m2,
∵AO=-x1,OB=x2,
∵
-
=
,
∴
-
=
,
∴
=
,
∴
=
,
解得m=2,经检验,m=2是方程的解.
∴所求抛物线的解析式为y=x2+2x-3.
∴m≠0.
令x2-mx+
| m2 |
| 2 |
∴△1=(-m)2-4×
| m2 |
| 2 |
令x2+mx-
| 3 |
| 4 |
∵△2=m2-4(-
| 3 |
| 4 |
∴抛物线y=x2+mx-
| 3 |
| 4 |
(2)设点A(x1,0),B(x2,0),
则x1、x2是方程x2+mx-
| 3 |
| 4 |
∴x1+x2=-m,x1•x2=-
| 3 |
| 4 |
∵AO=-x1,OB=x2,
∵
| 1 |
| OB |
| 1 |
| AO |
| 2 |
| 3 |
∴
| 1 |
| x2 |
| 1 |
| -x1 |
| 2 |
| 3 |
∴
| x1+x2 |
| x1•x2 |
| 2 |
| 3 |
∴
| -m | ||
-
|
| 2 |
| 3 |
解得m=2,经检验,m=2是方程的解.
∴所求抛物线的解析式为y=x2+2x-3.
点评:本题主要考查了二次函数与一元二次方程的联系.

练习册系列答案
相关题目