题目内容
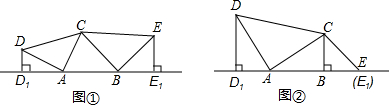
如图①所示,已知A,B为直线l上两点,点C为直线l上方一动点,连接AC、BC,分别以AC、BC为直角边向△ABC外作等腰直角△CAD和等腰直角△CBE,满足∠CAD=∠CBE=90°,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.
(1)如图②,当点E恰好在直线l上时,试说明DD1=AB;
(2)在图①中,当D,E两点都在直线l的上方时,试探求三条线段DD1,EE1,AB之间的数量关系,并说明理由.
解:(1)∵△CAD、△CBE是等腰直角三角形,且∠CAD=∠CBE=90°,
∴AC=AD,BC=BE,
∴∠ABC=90°.∠DAD1+∠CAB=90°.
∵DD1⊥l,
∴∠DD1A=90°,
∴∠DD1A=∠ABC.
∵∠CAB+∠ACB=90°,
∴∠DAD1=∠ACB.
在△ADD1和△CAB中,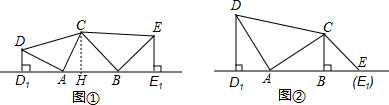
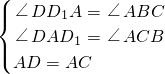 ,
,
∴△ADD1≌△CAB(AAS),
∴DD1=AB;
(2)DD1,EE1,AB之间的数量关系是:DD1+EE1=AB
理由:过点C作CH⊥l于H,
由(1)得△DD1A≌△AHC,△CHB≌△EE1B,
∴AH=DD1,HB=EE1,
∴AH+HB=DD1+EE1,
即AB=DD1+EE1.
分析:(1)由条件可以得出∠ABC=90°,∠DD1A=90°,根据等腰直角三角形的性质就可以得出AD=AC,∠DAC=90°,就可以得出∠DAD1=∠ACB,从而得出△ADD1≌△CAB就可以得出结论;
(2)过点C作CH⊥l于H,通过证明△DD1A≌△AHC,△CHB≌△EE1B,就可以得出AH=DD1,HB=EE1,从而得出.
点评:本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时运用三角形全等制造相等线段是关键.
∴AC=AD,BC=BE,
∴∠ABC=90°.∠DAD1+∠CAB=90°.
∵DD1⊥l,
∴∠DD1A=90°,
∴∠DD1A=∠ABC.
∵∠CAB+∠ACB=90°,
∴∠DAD1=∠ACB.
在△ADD1和△CAB中,

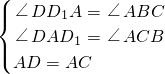 ,
,∴△ADD1≌△CAB(AAS),
∴DD1=AB;
(2)DD1,EE1,AB之间的数量关系是:DD1+EE1=AB
理由:过点C作CH⊥l于H,
由(1)得△DD1A≌△AHC,△CHB≌△EE1B,
∴AH=DD1,HB=EE1,
∴AH+HB=DD1+EE1,
即AB=DD1+EE1.
分析:(1)由条件可以得出∠ABC=90°,∠DD1A=90°,根据等腰直角三角形的性质就可以得出AD=AC,∠DAC=90°,就可以得出∠DAD1=∠ACB,从而得出△ADD1≌△CAB就可以得出结论;
(2)过点C作CH⊥l于H,通过证明△DD1A≌△AHC,△CHB≌△EE1B,就可以得出AH=DD1,HB=EE1,从而得出.
点评:本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时运用三角形全等制造相等线段是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 20、如图9所示,已知:∠α、线段a,求作等腰三角形△ABC,使腰长AB=a,底角∠A=∠α.(要求写出作法,并保留作图痕迹)
20、如图9所示,已知:∠α、线段a,求作等腰三角形△ABC,使腰长AB=a,底角∠A=∠α.(要求写出作法,并保留作图痕迹) (2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
(2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
 所示.已知展开图中每个正方形的边长为1.
所示.已知展开图中每个正方形的边长为1.