题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一动点,
上一动点,
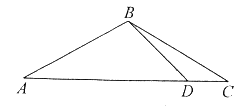
(1)![]() 的长
的长![]() ____________;
____________;
(2)![]() 的最小值是___________.
的最小值是___________.
【答案】![]() ;
; ![]()
【解析】
(1)过点B作BE⊥AC于点E,根据等腰三角形的性质得出AE=CE=![]() AC,再根据
AC,再根据![]() 利用锐角三角函数即可求得.
利用锐角三角函数即可求得.
(2)过点B作BE⊥AC于点E,延长BE到M使BE=ME,过M点作MN⊥BC于N,交AC于点D,则点D即为所求,再根据垂直平分线的性质和锐角三角函数求出MN的长即可.
(1)解:过点B作BE⊥AC于点E,
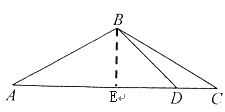
∵![]()
∴AC=2AE,
在Rt![]() ABE中,∠HEB=90°,
ABE中,∠HEB=90°,![]()
∴AE=ABcos![]() =4
=4![]() =2
=2![]() ,BE=2
,BE=2
∴AC=4![]()
故答案为:4![]() .
.
(2)过点B作BE⊥AC于点E,延长BE到M使BE=ME,过M点作MN⊥BC于N,交AC于点D,连接DB,则![]() 的最小.
的最小.

∵MN⊥BC,∴∠CND=90°,
∵![]() ,∴DN=
,∴DN=![]() CD
CD
∴![]()
∵BE⊥AC,BE=ME,
∴BD=MD,
∴![]() ,
,
∵BE⊥AC,![]()
∴∠CBM=60°,
∵BM=2BE=4,在Rt![]() BMN中,MN=BMsin60°=4
BMN中,MN=BMsin60°=4![]() =2
=2![]()
∴![]() 的最小值为2
的最小值为2![]()
故答案为:2![]()

练习册系列答案
相关题目