Question

【题目】如图，已知：AC=BC，AC⊥BC，AE⊥CF，BF⊥CF，C、E、F分别为垂足， 且∠BCF=∠ABF，CF交AB于D.

（1）判断△BCF≌△CAE，并说明理由.

（2）判断△ADC是不是等腰三角形？并说明理由.

Answer 1

【答案】（1）△BCF≌△CAE．理由见解析；

（2）△ADC是等腰三角形．理由见解析.

【解析】（1）解：△BCF≌△CAE．理由如下：

∵AC⊥BC，AE⊥CF，

∴∠ACE+∠BCF=90°，∠ACE+∠CAE=90°，

∴∠CAE=∠BCF，

∵AE⊥CF，BF⊥CF，

∴∠AEC=∠F=90°，

在△BCF和△CAE中，

∵，

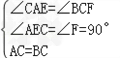∴△BCF≌△CAE（AAS）；

（2）解：△ADC是等腰三角形．理由如下：

∵AC⊥BC，BF⊥CF，

∴∠ACB=∠F=90°，

∴∠ACD+∠BCF=90°，∠BDF+∠ABF=90°，

∵∠BCF=∠ABF，

∴∠ACD=∠BDF，

又∵∠BDF=∠ADC（对顶角相等），

∴∠ACD=∠ADC，

∴AC=AD，

故△ADC是等腰三角形。