Question

已知：抛物线y=-

1

2

x²-（m+3）x+m²-12与x轴交于A（x₁，0）、B（x₂，0）两点，且x₁＜0，x₂＞0，抛物线与y轴交于点C，OB=2OA．
（1）求抛物线的解析式；
（2）在x轴上，点A的左侧，求一点E，使△ECO与△CAO相似，并说明直线EC经过（1）中抛物线的顶点D；
（3）过（2）中的点E的直线y=

1

4

x+b与（1）中的抛物线相交于M、N两点，分别过M、N作x轴的垂线，垂足为M′、N′，点P为线段MN上一点，点P的横坐标为t，过点P作平行于y轴的直线交（1）中所求抛物线于点Q．是否存在t值，使S_梯形MM'N'N：S_△QMN=35：12？若存在，求出满足条件的t值；若不存在，请说明理由．

Answer 1

分析：（1）可设出A、B的坐标，然后用韦达定理表示出两点横坐标的和与积，然后根据OB=2OA，即B点的横坐标为A点横坐标的2倍联立三式可得出m的值．即可求出抛物线的解析式；
（2）根据△ECO与△CAO相似，可通过相似三角形的对应边成比例线段求出OE的长，即可得出E点的坐标，进而可求出过E点直线的解析式，然后将抛物线顶点代入直线的解析式中进行判断即可；
（3）过M、N分别作直线PQ的垂线后可发现，三角形QMN可以以QP为底，以M、N两点的横坐标差为高来求得其面积，而梯形的面积可以以M、N两点的纵坐标的和与两点横坐标的差为高来求，因此三角形QMN和梯形的面积比实际是QM和M、N两点的纵坐标的比．可联立直线MN与抛物线的解析式求出M、N两点纵坐标的和，然后将t代入抛物线和直线MN的解析式中求出QP的表达式，根据题中给出的两个图形的面积比即可求得t的值．

解答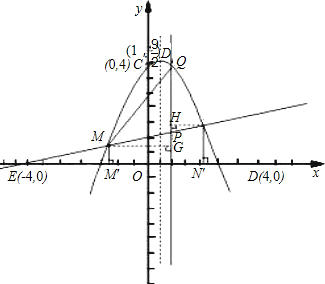：解：（1）∵x₁＜0，x₂＞0．
∴OA=x₁，OB=x₂
∵x₁，x₂是方程-

1

2

x²-（m+3）x+m²-12=0的两个实数根
∴x₁+x₂=-2（m+3）①，x₁•x₂=-2（m²-12）②x₂=-2x₁③
联立①，②，③整理得：m²+8m+16=0，
解得m=-4．
∴抛物线的解析式为y=-x²+x+4；

（2）设点E（x，0），则OE=-x．
∵△ECO与△CAO相似，
∴

OC

OE

=

OA

OC

，

4

-x

=

2

4

，x=-8
∴点E（-8，0）
设过E、C两点的直线解析式为y=k′x+b′，
则有：

-8k′+b′=0 b′=4

，
解得

k′= 1 2 b′=4

∴直线EC的解析式为y=

1

2

x+4．
∵抛物线的顶点D（1，

9

2

），当x=1时，y=

9

2

∴点D在直线EC上；

（3）存在t值，使S_梯形MM'N'N：S_△QMN=35：12．
∵E（-8，0），
∴

1

4

×（-8）+b=0，
∴b=2，y=

1

4

x+2．
∴x=4（y-2）．
∴y=-

1

2

[4（y-2）²+4（y-2）+4]，
整理得8y²-35y+6=0，
设M（x_m，y_m）．
∴MM′=y_m，NN′=y_n，
∴y_m，y_n是方程8y²-35y+6=0的两个实数根，y_m+y_n=

35

8

∴S_梯形=

1

2

（y_m+y_n）（x_n-x_m）
∵点P在直线y=

1

4

x+2上，点Q在（1）中抛物线上，
∴点P（t，

1

4

t+2）、点Q（t，-

1

2

t²+t+4）
∴PQ=-

1

2

t²+t+4-

1

4

t-2=-

1

2

t²-

3

4

t+2，
分别过M、N作直线PQ的垂线，垂足为G、H，则GM=t-x_m，NH=x_n-t
∴S_△QMN=S_△QMP+S_△QNP=

1

2

PQ（x_n-x_m）
∵S_梯形MM'N'N：S_△QMN=35：12，
∴

1 2 (ym+yn)(xn-xm)

1 2 (- 1 2 t2- 3 4 t+2)(xn-xm)

=

12

35

，
整理得：2t²-3t-2=0，
解得t=-

1

2

，t=2．
因此当t=-

1

2

或t=2时，S_梯形MM'N'N：S_△QMN=35：12．

点评：本题为二次函数综合题，考查了二次函数解析式的确定、图形面积的求法、函数图象交点等知识点，难度较大．