题目内容
如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2
，则阴影部分图形的面积为（ ）
| 3 |
| A．4π | B．2π | C．π | D．
|
连接OD．
∵CD⊥AB，
∴CE=DE=
CD=
（垂径定理），
故S△OCE=S△ODE，
即可得阴影部分的面积等于扇形OBD的面积，
又∵∠CDB=30°，
∴∠COB=60°（圆周角定理），
∴OC=2，
故S扇形OBD=
=
，即阴影部分的面积为
．
故选D．
∵CD⊥AB，∴CE=DE=
| 1 |
| 2 |
| 3 |
故S△OCE=S△ODE，
即可得阴影部分的面积等于扇形OBD的面积，
又∵∠CDB=30°，
∴∠COB=60°（圆周角定理），
∴OC=2，
故S扇形OBD=
| 60π×22 |
| 360 |
| 2π |
| 3 |
| 2π |
| 3 |
故选D．
练习册系列答案
相关题目
转90°得到线段AC．
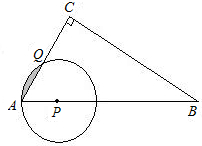以点P为圆心，PA为半径画⊙P交AC于点Q．