题目内容
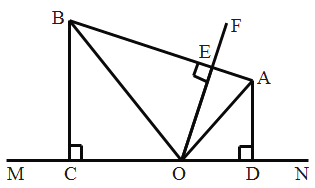
【题目】如图,矩形OABC的顶点O与平面直角坐标系的原点重合,点A,C分别在x轴,y轴上,点B的坐标为(-5,4),点D为边BC上一点,连接OD,若线段OD绕点D顺时针旋转90°后,点O恰好落在AB边上的点E处,则点E的坐标为( )

A. (-5,3) B. (-5,4) C. (-5,![]() ) D. (-5,2)
) D. (-5,2)
【答案】A
【解析】
先判定△DBE≌△OCD,可得BD=OC=4,设AE=x,则BE=4﹣x=CD,依据BD+CD=5,可得4+4﹣x=5,进而得到AE=3,据此可得E(﹣5,3).
由题可得:AO=BC=5,AB=CO=4,由旋转可得:DE=OD,∠EDO=90°.
又∵∠B=∠OCD=90°,∴∠EDB+∠CDO=90°=∠COD+∠CDO,∴∠EDB=∠DOC,∴△DBE≌△OCD,∴BD=OC=4,设AE=x,则BE=4﹣x=CD.
∵BD+CD=5,∴4+4﹣x=5,解得:x=3,∴AE=3,∴E(﹣5,3).
故选A.

练习册系列答案
相关题目
【题目】一只不透明的袋子中装有![]() 个相同小球,分别标有不等的自然数
个相同小球,分别标有不等的自然数![]() 、
、![]() 、
、![]() 、
、![]() ,小丽每次从袋中同时摸出
,小丽每次从袋中同时摸出![]() 个小球,并计算摸出的这
个小球,并计算摸出的这![]() 个小球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:
个小球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:
摸球总次数 |
|
|
|
|
|
|
|
|
|
|
“和为 |
|
|
|
|
|
|
|
|
|
|
“和为 |
|
|
|
|
|
|
|
|
|
|
![]() 如果实验继续进行下去,出现“和为
如果实验继续进行下去,出现“和为![]() ”的频率将稳定在它的概率附近.试估计出现“和为
”的频率将稳定在它的概率附近.试估计出现“和为![]() ”的概率;
”的概率;
![]() 根据
根据![]() 中结论,求出自然数
中结论,求出自然数![]() 的值.
的值.