题目内容
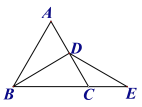
【题目】如图,△ABC中,AC的垂直平分线DE与∠ABC的角平分线相交于点D,垂足为点E,若∠ABC=72°,求∠ADC的度数.

【答案】108°
【解析】
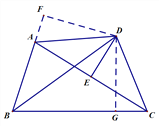
试题分析:根据角平分线的性质, 过点D作DF⊥BA延长线于点F,DG⊥BC于点G,然后利用HL证明Rt△DAF≌Rt△DGC,可得: ∠FDA=∠GDC,根据四边形内角和即可求解.
试题解析:过点D作DF⊥BA延长线于点F,G⊥BC于点G,
所以∠DFA=∠DGC=90°,
又因为AD平分∠ABC,
所以DF=DG,
因为DE垂直平分AC,
所以DA=DC,
在Rt△DAF和Rt△DGC中,
![]() ,
,
所以Rt△DAF≌Rt△DGC(HL),
所以∠FDA=∠GDC,
所以∠ADC=∠FDG=360°-∠DFA-∠DGC-∠ADC=360°-90°-90°-72°=108°.

练习册系列答案
相关题目