题目内容
设抛物线y=ax2+bx-2与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C,且∠ACB=90°。
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线y=x+1交抛物线于另一点E,若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标;
(3)在(2)的条件下,△BDP的外接圆半径等于_____________。
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线y=x+1交抛物线于另一点E,若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标;
(3)在(2)的条件下,△BDP的外接圆半径等于_____________。
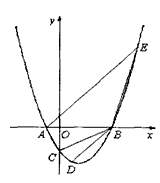
解:(1)令x=0,得y=-2,
∴C(0,-2),
∵∠ACB=90°,CO⊥AB,
∴△AOC∽△COB,
∴OA·OB=OC2,
∴OB=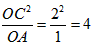 ,
,
∴m=4,
将A(-1,0),B(4,0)代入y=ax2+bx-2,得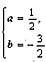 ,
,
∴抛物线的解析式为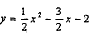 ;
;
(2)D(1,n)代入y=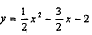 ,得n=-3,
,得n=-3,
由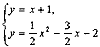 ,得
,得
∴E(6,7)过E作EH⊥x轴于H,则H(6,0)
∴AH=EH=7
∴∠EAH=45°
过D作DF⊥x轴于F,则F(1,0)
∴BF=DF=3
∴∠DBF=45°
∴∠EAH=∠DBF=45°
∴∠DBH=135°,90°<∠EBA<135°
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,
则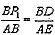
∴BP1=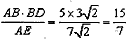
∴OP1=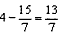 ,
,
∴P1(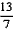 ,0)
,0)
②若△DBP2∽△BAE,
则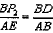
∴BP2=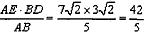
∴OP2=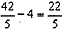
∴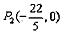
综合①、②,得点P的坐标为: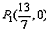 或
或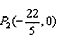 ;
;
(3)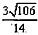 或
或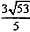 。
。
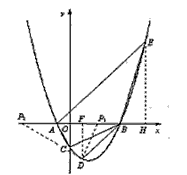
∴C(0,-2),
∵∠ACB=90°,CO⊥AB,
∴△AOC∽△COB,
∴OA·OB=OC2,
∴OB=
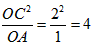 ,
, ∴m=4,
将A(-1,0),B(4,0)代入y=ax2+bx-2,得
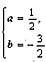 ,
,∴抛物线的解析式为
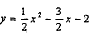 ;
;(2)D(1,n)代入y=
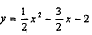 ,得n=-3,
,得n=-3,由
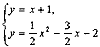 ,得
,得
∴E(6,7)过E作EH⊥x轴于H,则H(6,0)
∴AH=EH=7
∴∠EAH=45°
过D作DF⊥x轴于F,则F(1,0)
∴BF=DF=3
∴∠DBF=45°
∴∠EAH=∠DBF=45°
∴∠DBH=135°,90°<∠EBA<135°
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,
则
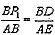
∴BP1=
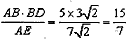
∴OP1=
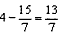 ,
, ∴P1(
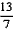 ,0)
,0)②若△DBP2∽△BAE,
则
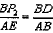
∴BP2=
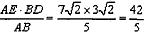
∴OP2=
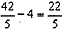
∴
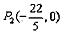
综合①、②,得点P的坐标为:
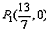 或
或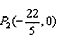 ;
;(3)
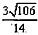 或
或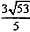 。
。

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
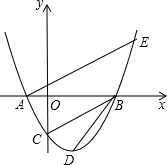 ACB=90度.
ACB=90度.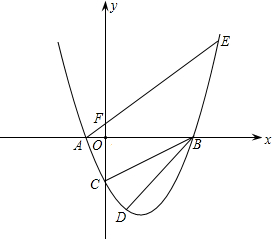 ,0),与y轴交于点C(0,-2),且∠ACB=90度.
,0),与y轴交于点C(0,-2),且∠ACB=90度.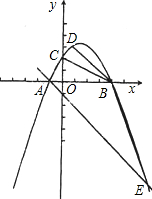 设抛物线y=ax2+bx+c与x轴交于两个不同的点A(-l,0)、B(4,0),与y轴交于点C(0,2).
设抛物线y=ax2+bx+c与x轴交于两个不同的点A(-l,0)、B(4,0),与y轴交于点C(0,2). m2-mb+n),其中 a,b,c,m,n为实数,且a,m不为0.
m2-mb+n),其中 a,b,c,m,n为实数,且a,m不为0.