题目内容
设抛物线y=ax2+bx-2与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C,且∠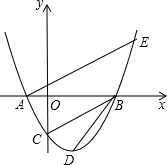 ACB=90度.
ACB=90度.(1)求m的值和抛物线的解析式;
(2)已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标;
(3)在(2)的条件下,△BDP的外接圆半径等于
分析:(1)根据抛物线的解析式可知C点坐标为(0,-2),即OC=2,由于∠ACB=90度,根据射影定理OC2=OA•AB,可求出AB的长,进而可求出B点的坐标,也就求出了m的值,然后将A、B的坐标代入抛物线中即可求出其解析式.
(2)可先根据抛物线的解析式和直线AE的解析式求出E点和D点的坐标,经过求解不难得出∠FDB=∠DBO=45°,因此本题要分两种情况进行讨论:①∠DPB=∠ABE;②∠PDB=∠ABE.可根据对应的相似三角形得出的成比例线段求出OP的长,进而可求出P点的坐标.
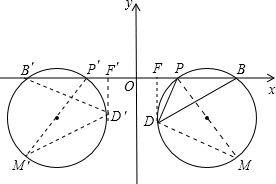
(3)以求△BP1D的外接圆半径为列进行说明:先作△BPD的外接圆,过P作直径PM,连接DM,那么不难得出△PMD和△FBD相似,可得出
=
,可先求出DP,DF,BD的长,而PM是圆的直径,由此可求出△BPD的外接圆的半径.
(2)可先根据抛物线的解析式和直线AE的解析式求出E点和D点的坐标,经过求解不难得出∠FDB=∠DBO=45°,因此本题要分两种情况进行讨论:①∠DPB=∠ABE;②∠PDB=∠ABE.可根据对应的相似三角形得出的成比例线段求出OP的长,进而可求出P点的坐标.
(3)以求△BP1D的外接圆半径为列进行说明:先作△BPD的外接圆,过P作直径PM,连接DM,那么不难得出△PMD和△FBD相似,可得出
| DP |
| PM |
| DF |
| BD |
解答: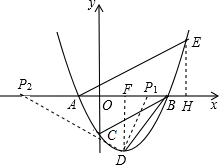 解:(1)令x=0,得y=-2,
解:(1)令x=0,得y=-2,
∴C(0,-2),
∵∠ACB=90°,CO⊥AB,
∴△AOC∽△COB,
∴OA•OB=OC2
∴OB=
=
=4,
∴m=4,
将A(-1,0),B(4,0)代入y=ax2+bx-2,
得
,
∴抛物线的解析式为y=
x2-
x-2.
(2)D(1,n)代入y=
x2-
x-2,得n=-3,
由
,得
,
,
∴E(6,7),
过E作EH⊥x轴于H,则H(6,0)
∴AH=EH=7
∴∠EAH=45°
过D作DF⊥x轴于F,则F(1,0)
∴BF=DF=3
∴∠DBF=45°
∴∠EAH=∠DBF=45°
∴∠DBH=135°,
90°<∠EBA<135°
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,则
=
∴BP1=
=
=
∴OP1=4-
=
,
∴P1(
,0).
②若△DBP2∽△BAE,则
=
∴BP2=
=
=
∴OP2=
-4=
∴P2(-
,0).
综合①、②,得点P的坐标为:P1(
,0)或P2(-
,0).
(3)
或
.
如图所示:先作△BPD的外接圆,过P作直径PM,连接DM,
∵∠PMD=∠PBD,∠DFP=∠PDM,
∴△PMD和△FBD相似,
 ∴
∴
=
,
∴PD=
=
=
,
DF=3,
BD=
=3
,
∴PM=
=
,
∴△BPD的外接圆的半径=
;
同理可求出当P点在x轴的负半轴上时,△BPD的外接圆的半径=
.
 解:(1)令x=0,得y=-2,
解:(1)令x=0,得y=-2,∴C(0,-2),
∵∠ACB=90°,CO⊥AB,
∴△AOC∽△COB,
∴OA•OB=OC2
∴OB=
| OC2 |
| OA |
| 22 |
| 1 |
∴m=4,
将A(-1,0),B(4,0)代入y=ax2+bx-2,
得
|
∴抛物线的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)D(1,n)代入y=
| 1 |
| 2 |
| 3 |
| 2 |
由
|
|
|
∴E(6,7),
过E作EH⊥x轴于H,则H(6,0)
∴AH=EH=7
∴∠EAH=45°
过D作DF⊥x轴于F,则F(1,0)
∴BF=DF=3
∴∠DBF=45°
∴∠EAH=∠DBF=45°
∴∠DBH=135°,
90°<∠EBA<135°
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,则
| BP1 |
| AB |
| BD |
| AE |
∴BP1=
| AB•BD |
| AE |
5×3
| ||
7
|
| 15 |
| 7 |
∴OP1=4-
| 15 |
| 7 |
| 13 |
| 7 |
∴P1(
| 13 |
| 7 |
②若△DBP2∽△BAE,则
| BP2 |
| AE |
| BD |
| AB |
∴BP2=
| AE•BD |
| AB |
7
| ||||
| 5 |
| 42 |
| 5 |
∴OP2=
| 42 |
| 5 |
| 22 |
| 5 |
∴P2(-
| 22 |
| 5 |
综合①、②,得点P的坐标为:P1(
| 13 |
| 7 |
| 22 |
| 5 |
(3)
3
| ||
| 14 |
3
| ||
| 5 |
如图所示:先作△BPD的外接圆,过P作直径PM,连接DM,
∵∠PMD=∠PBD,∠DFP=∠PDM,
∴△PMD和△FBD相似,
 ∴
∴| DP |
| PM |
| DF |
| BD |
∴PD=
(
|
|
3
| ||
| 7 |
DF=3,
BD=
| (1-4)2+(-3)2 |
| 2 |
∴PM=
| DP•BD |
| DF |
3
| ||
| 7 |
∴△BPD的外接圆的半径=
3
| ||
| 14 |
同理可求出当P点在x轴的负半轴上时,△BPD的外接圆的半径=
3
| ||
| 5 |
点评:本题考查二次函数解析式的确定、函数图象交点、三角形相似以及△外接圆的半径的求法等知识及综合应用知识、解决问题的能力.
(要注意区别三角形内切圆和外接圆半径求法的不同:三角形内切圆半径通常用公式法求解.而三角形外接圆半径通常要通过构建相似三角形来求解).
(要注意区别三角形内切圆和外接圆半径求法的不同:三角形内切圆半径通常用公式法求解.而三角形外接圆半径通常要通过构建相似三角形来求解).

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
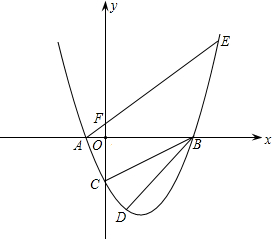 ,0),与y轴交于点C(0,-2),且∠ACB=90度.
,0),与y轴交于点C(0,-2),且∠ACB=90度.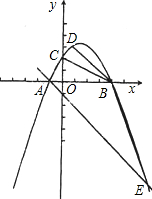 设抛物线y=ax2+bx+c与x轴交于两个不同的点A(-l,0)、B(4,0),与y轴交于点C(0,2).
设抛物线y=ax2+bx+c与x轴交于两个不同的点A(-l,0)、B(4,0),与y轴交于点C(0,2). m2-mb+n),其中 a,b,c,m,n为实数,且a,m不为0.
m2-mb+n),其中 a,b,c,m,n为实数,且a,m不为0.