题目内容
【题目】如图:![]() 中,
中,![]() .
.

![]() 求作
求作![]() 边上的垂直平分线
边上的垂直平分线![]() ,使得
,使得![]() 交
交![]() 于
于![]() ;将线段
;将线段![]() 沿着
沿着![]() 的方向平移到线段
的方向平移到线段![]() (其中点
(其中点![]() 平移到点
平移到点![]() ,画出平移后的线段
,画出平移后的线段![]() ;(要求用尺规作图,不写作法,保留作图痕迹.)
;(要求用尺规作图,不写作法,保留作图痕迹.)
![]() 连接
连接![]() 、
、![]() ,试判断四边形
,试判断四边形![]() 是矩形吗?说明理由.
是矩形吗?说明理由.
【答案】 (1)作图见解析;(2)证明见解析.
【解析】
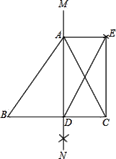
(1)以B,C为圆心,大于![]() BC长为半径化弧,两弧交于一点,过A与这一点作直线MN,MN为所求的BC的垂直平分线;以D为圆心,AB长为半径化弧,再以A为圆心,BD长为半径化弧,两弧交于一点E,连接DE,线段DE为平移后的线段;
BC长为半径化弧,两弧交于一点,过A与这一点作直线MN,MN为所求的BC的垂直平分线;以D为圆心,AB长为半径化弧,再以A为圆心,BD长为半径化弧,两弧交于一点E,连接DE,线段DE为平移后的线段;
(2)首先证明四边形ADCE为平行四边形,再证明对角线AC=DE,可证出要求的结论.
![]() 如图,
如图,![]() 为所求的
为所求的![]() 的垂直平分线;
的垂直平分线;
线段![]() 为平移后的线段;
为平移后的线段;
![]() 四边形
四边形![]() 为矩形,理由如下:
为矩形,理由如下:
由平移的特征得:![]() ,
,![]() 且
且![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() 且
且![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∵![]() ,
,
∴![]() ,
,
∴平行四边形![]() 为矩形.
为矩形.

练习册系列答案
相关题目