题目内容
在Rt△ABC中,∠C=90°,BC=6cm,∠ABC=30°.D是CB上一点,DC=1cm.P、Q是直线CB上的两个动点,点P从C点出发,以1cm/s的速度沿直线CB向右运动,同时,点Q从D点出发,以2cm/s的速度沿直线CB向右运动,以PQ为一边在CB的上方作等边三角形PQR,下图是其运动过程中的某一位置.设运动的时间是t(s).
(1)△PQR的边长是______cm(用含有t的代数式表示);
(2)若等边△PQR与△ABC重叠部分的面积为y(cm2),求y与t之间的函数关系式,并写出自变量t的取值范围.
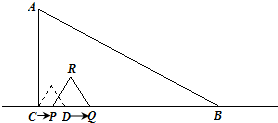
解:(1)△PQR的边长PQ=CQ-CP=(CD+DP)-CP=(1+2t)-t=(t+1)cm;
故答案为:(t+1);
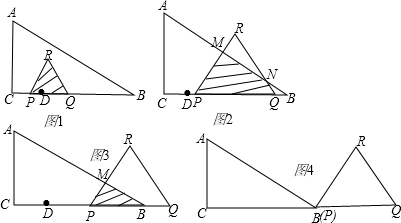
(2)当0≤t< 时,如图1:易得重叠部分为一个小等边三角形其边长为t+1,
时,如图1:易得重叠部分为一个小等边三角形其边长为t+1,
则重叠部分的面积y= (t+1)2;
(t+1)2;
当 ≤t<
≤t< 时,如图2:易得重叠部分为四边形MNQP,
时,如图2:易得重叠部分为四边形MNQP,
∵∠B=30°,且△RPQ为等边三角形,得到∠RPQ=∠R=60°,
∴∠PMN=90°,且PB=BC-CP=6-t,∠RNM=30°,
∴PM= (6-t),故MR=PR-PM=(t+1)-
(6-t),故MR=PR-PM=(t+1)- (6-t)=
(6-t)= (3t-4),
(3t-4),
∴MN=MR•tan60°= (3t-4),
(3t-4),
则重叠部分的面积y= (t+1)2-
(t+1)2- (3t-4)2
(3t-4)2
=-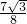 t2+
t2+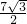 t-
t-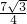
=-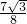 (t-2)2+
(t-2)2+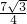 ;
;
当 ≤t<6时,如图3:同理可得y=
≤t<6时,如图3:同理可得y= (6-t)2;
(6-t)2;
当t≥6时,如图4:可得y=0.
分析:(1)根据题意,直接将△PQR的三边相加即可得出含t的表达式;易得△QRB为等腰三角形,可得到QB=QR=QP=t+1;
(2)易得重叠部分为一个小等边三角形,依题意根据重叠部分图形的形状分四种情况考虑:如图分别画出图形,图形1根据等边三角形的边长为t+1,表示出重叠部分的面积y;图形2,用等边三角形RPQ的面积减去三角形RMN的面积,首先由等边三角形的性质得到内角为60°,再由∠B=30°可得MN与RP垂直,可得三角形RMN为直角三角形,由30°所对的直角边等于斜边的一半,先表示出PB的长,进而表示出MP的长,用RP-MP可得PM的长,再利用锐角三角函数表示出MN的长,即可表示出三角形RMN的面积,可表示出重叠部分的面积;图形3,同理可得重叠部分的面积;图形4,根据图形可得重叠部分的面积为0.
点评:本题考查了等边三角形的性质,直角三角形的性质,以及相似三角形的判定与性质,是一道动态几何题,综合性较强,有一定的难度.特别是第二问动点P和Q运动过程中,与三角形ABC重叠部分存在四种情况,学生应借助图形,利用分类讨论的思想来解决问题.
故答案为:(t+1);

(2)当0≤t<
 时,如图1:易得重叠部分为一个小等边三角形其边长为t+1,
时,如图1:易得重叠部分为一个小等边三角形其边长为t+1,则重叠部分的面积y=
 (t+1)2;
(t+1)2;当
 ≤t<
≤t< 时,如图2:易得重叠部分为四边形MNQP,
时,如图2:易得重叠部分为四边形MNQP,∵∠B=30°,且△RPQ为等边三角形,得到∠RPQ=∠R=60°,
∴∠PMN=90°,且PB=BC-CP=6-t,∠RNM=30°,
∴PM=
 (6-t),故MR=PR-PM=(t+1)-
(6-t),故MR=PR-PM=(t+1)- (6-t)=
(6-t)= (3t-4),
(3t-4),∴MN=MR•tan60°=
 (3t-4),
(3t-4),则重叠部分的面积y=
 (t+1)2-
(t+1)2- (3t-4)2
(3t-4)2=-
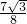 t2+
t2+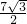 t-
t-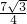
=-
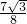 (t-2)2+
(t-2)2+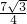 ;
;当
 ≤t<6时,如图3:同理可得y=
≤t<6时,如图3:同理可得y= (6-t)2;
(6-t)2;当t≥6时,如图4:可得y=0.
分析:(1)根据题意,直接将△PQR的三边相加即可得出含t的表达式;易得△QRB为等腰三角形,可得到QB=QR=QP=t+1;
(2)易得重叠部分为一个小等边三角形,依题意根据重叠部分图形的形状分四种情况考虑:如图分别画出图形,图形1根据等边三角形的边长为t+1,表示出重叠部分的面积y;图形2,用等边三角形RPQ的面积减去三角形RMN的面积,首先由等边三角形的性质得到内角为60°,再由∠B=30°可得MN与RP垂直,可得三角形RMN为直角三角形,由30°所对的直角边等于斜边的一半,先表示出PB的长,进而表示出MP的长,用RP-MP可得PM的长,再利用锐角三角函数表示出MN的长,即可表示出三角形RMN的面积,可表示出重叠部分的面积;图形3,同理可得重叠部分的面积;图形4,根据图形可得重叠部分的面积为0.
点评:本题考查了等边三角形的性质,直角三角形的性质,以及相似三角形的判定与性质,是一道动态几何题,综合性较强,有一定的难度.特别是第二问动点P和Q运动过程中,与三角形ABC重叠部分存在四种情况,学生应借助图形,利用分类讨论的思想来解决问题.

练习册系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )