题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() ,
,![]() 在
在![]() ,
,![]() 上,且
上,且![]() .
.
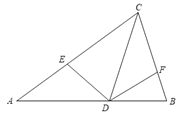
(1)求![]() 的度数;
的度数;
(2)求证:![]() .
.
【答案】(1)108°;(2)见解析
【解析】
(1)由等腰三角形的性质和三角形内角和定理得出∠B=∠ACB=72°,由角平分线定义得出∠ACD=∠BCD=36°,由三角形的外角性质即可得出答案;
(2)由(1)得∠ACD=36°=∠A,∠ADC=108°,得出AD=CD,证出∠ADC=∠EDF,得出∠ADE=∠CDF,证明△ADE≌△CDF(ASA),得出AE=CF,即可得出结论.
(1)解:∵AB=AC,∠A=36°,
∴∠B=∠ACB=![]() (180°-36°)=72°,
(180°-36°)=72°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=36°,
∴∠ADC=∠B+∠BCD=72°+36°=108°;
(2)证明:由(1)得:∠ACD=36°=∠A,∠ADC=108°,
∴AD=CD,
∵∠EDF=108°,
∴∠ADC=∠EDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
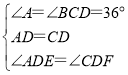 ,
,
∴△ADE≌△CDF(ASA),
∴AE=CF,
∵CF+BF=BC,
∴AE+BF=BC.

练习册系列答案
相关题目






