题目内容
如图,在矩形ABCD中,由8个面积均为1的小正方形组成的L形模板如图放置,则矩形ABCD的周长为__________.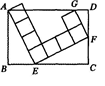

8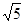
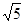
连接AF,作GH⊥AE于点H,则有AE=EF=HG=4,FG=2,AH=2,根据矩形的性质及勾股定理即可求得其周长.
解:如图,连接AF,作GH⊥AE于点H,则有AE=EF=HG=4,FG=2,AH=2,
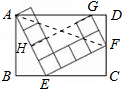
∵AG=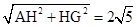 ,AF=
,AF=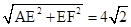 ,
,
∴AF2=AD2+DF2=(AG+GD)2+FD2=AG2+GD2+2AG?GD+FD2,GD2+FD2=FG2
∴AF2=AG2+2AG?GD+FG2∴32=20+2×2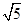 ×GD+4,
×GD+4,
∴GD=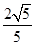 ,FD=
,FD=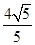 ,
,
∵∠BAE+∠AEB=90°=∠FEC+∠AEB,
∴∠BAE=∠FEC,
∵∠B=∠C=90°,AE=EF,
∴△ABE≌△ECF,
∴AB=CE,CF=BE,
∵BC=BE+CE=AD=AG+GD=2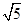 +
+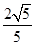 ,
,
∴AB+FC=2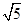 +
+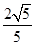
∴矩形ABCD的周长=AB+BC+AD+CD=2BC+AB+CF+DF
=2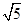 +
+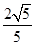 +2
+2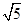 +
+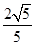 +2
+2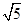 +
+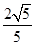 +
+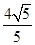 =8
=8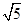 .
.
故答案为,8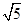
解:如图,连接AF,作GH⊥AE于点H,则有AE=EF=HG=4,FG=2,AH=2,

∵AG=
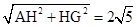 ,AF=
,AF=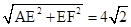 ,
,∴AF2=AD2+DF2=(AG+GD)2+FD2=AG2+GD2+2AG?GD+FD2,GD2+FD2=FG2
∴AF2=AG2+2AG?GD+FG2∴32=20+2×2
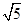 ×GD+4,
×GD+4,∴GD=
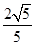 ,FD=
,FD=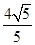 ,
,∵∠BAE+∠AEB=90°=∠FEC+∠AEB,
∴∠BAE=∠FEC,
∵∠B=∠C=90°,AE=EF,
∴△ABE≌△ECF,
∴AB=CE,CF=BE,
∵BC=BE+CE=AD=AG+GD=2
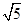 +
+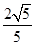 ,
,∴AB+FC=2
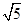 +
+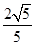
∴矩形ABCD的周长=AB+BC+AD+CD=2BC+AB+CF+DF
=2
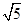 +
+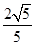 +2
+2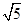 +
+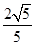 +2
+2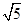 +
+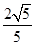 +
+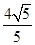 =8
=8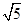 .
.故答案为,8
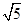

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目

 ,这个矩形的长宽各是多少?
,这个矩形的长宽各是多少?

 中,AE是BC边上的高,将
中,AE是BC边上的高,将 沿
沿 方向平移,使点E与点C重合,得
方向平移,使点E与点C重合,得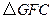 .
.
 ;
; ,当AB与BC满足什么数量关系时,四边形
,当AB与BC满足什么数量关系时,四边形 是菱形?证明你的结论.
是菱形?证明你的结论.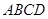 的边长是4cm,点
的边长是4cm,点 在边
在边 上,以
上,以 为边向外作正方形
为边向外作正方形 ,连结
,连结 、
、 、
、 ,则
,则 的面积是_____________cm2.
的面积是_____________cm2.
