题目内容
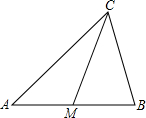 如图,已知CM是△ABC的边AB上的中线.
如图,已知CM是△ABC的边AB上的中线.(1)请你作出△AMC中AM边上的高;
(2)若△ABC的面积为40,求△BMC的面积;
(3)若AC=10cm,BC=8cm,求△ABD和△ACD周长之差是多少.
分析:(1)根据三角形高的作法得出即可;
(2)利用三角形中线平分三角形面积进而得出答案;
(3)利用△ACM与△BCM的周长之差是:AC+AM+CM-BM-CM-BC=AC-BC进而得出答案.
(2)利用三角形中线平分三角形面积进而得出答案;
(3)利用△ACM与△BCM的周长之差是:AC+AM+CM-BM-CM-BC=AC-BC进而得出答案.
解答: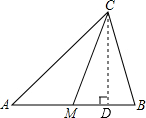 解:(1)如图所示:CD即为所求;
解:(1)如图所示:CD即为所求;
(2)∵CM是△ABC的边AB上的中线,
∴S△BMC=
S△ABC=20;
(3)△ACM与△BCM的周长之差是:AC+AM+CM-BM-CM-BC=AC-BC=2(cm).
 解:(1)如图所示:CD即为所求;
解:(1)如图所示:CD即为所求;(2)∵CM是△ABC的边AB上的中线,
∴S△BMC=
| 1 |
| 2 |
(3)△ACM与△BCM的周长之差是:AC+AM+CM-BM-CM-BC=AC-BC=2(cm).
点评:此题主要考查了三角形高的作法以及三角形中线的性质以及周长之间关系,熟练掌握三角形中线的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
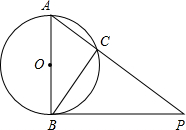 如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC=
如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC=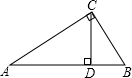 如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于
如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于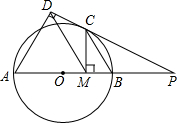 如图,已知AB是⊙O的直径,PC切⊙O于C,AD⊥PD,CM⊥AB,垂足分别为D,M.
如图,已知AB是⊙O的直径,PC切⊙O于C,AD⊥PD,CM⊥AB,垂足分别为D,M. (2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.