题目内容
 (2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.(1)求证:PC是⊙O的切线;
(2)若点M是
 | AB |
分析:(1)利用已知得出∠PCB+∠OCB=90°,进而求出∠PCO=90°,利用切线的判定定理求出即可;
(2)首先证明△MBN∽△MCB,再利用相似的性质求出△MBN∽△MCB,进而得出MN•MC=BM2的值.
(2)首先证明△MBN∽△MCB,再利用相似的性质求出△MBN∽△MCB,进而得出MN•MC=BM2的值.
解答: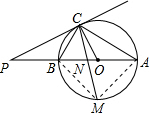 解:(1)∵OA=OC,
解:(1)∵OA=OC,
∴∠A=∠ACO,
∴∠COB=2∠A,
又∵∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACB=90°,即∠ACO+∠OCB=90°,
∴∠PCB+∠OCB=90°,即∠PCO=90°,
而OC是⊙O的半径,
∴PC是⊙O的切线.
(2)连接MA,MB,
∵点M是
的中点,
∴
=
,
∴∠BCM=∠ABM,而∠BMN=∠BMC,
∴△MBN∽△MCB,
∴
=
,
又∵AB是⊙O的直径,
=
,
∴∠AMB=90°,AM=BM.
∵AB=8,
∴BM=4
.
∴MN•MC=BM2=32.
 解:(1)∵OA=OC,
解:(1)∵OA=OC,∴∠A=∠ACO,
∴∠COB=2∠A,
又∵∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACB=90°,即∠ACO+∠OCB=90°,
∴∠PCB+∠OCB=90°,即∠PCO=90°,
而OC是⊙O的半径,
∴PC是⊙O的切线.
(2)连接MA,MB,
∵点M是
 |
| AB |
∴
 |
| AM |
 |
| BM |
∴∠BCM=∠ABM,而∠BMN=∠BMC,
∴△MBN∽△MCB,
∴
| BM |
| MC |
| MN |
| BM |
又∵AB是⊙O的直径,
 |
| AM |
 |
| BM |
∴∠AMB=90°,AM=BM.
∵AB=8,
∴BM=4
| 2 |
∴MN•MC=BM2=32.
点评:此题主要考查了切线的判定与相似三角形的判定与性质,此题是中考中重点题型同学们应重点掌握.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
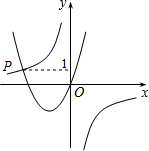 (2012•梁子湖区模拟)如图,已知函数
(2012•梁子湖区模拟)如图,已知函数 (2012•梁子湖区模拟)如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于N,且S△ABC=24,那么S四边形ANME-S△DMN=
(2012•梁子湖区模拟)如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于N,且S△ABC=24,那么S四边形ANME-S△DMN= (2012•梁子湖区模拟)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为( )
(2012•梁子湖区模拟)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为( )