题目内容
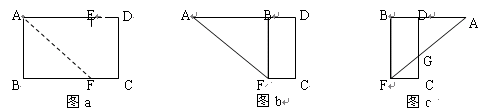
如图,大正方形中有2个小正方形，如果它们的面积分别是S1，S2，那么S1，S2的比值是（ ）
| A．1:1 | B．8:9 | C．9:8 | D． |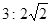
C
设正方形的边长为x，根据等腰直角三角形的性质知AC、BC的长，进而可求得S2的边长，由面积的求法可得答案．
如图，设正方形的边长为x，
根据等腰直角三角形的性质知，AC=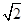
BC，BC=CE=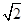CD，
∴AC=2CD，CD=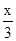
，
∴S2的边长为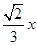
，S2的面积为
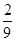x2，S1的边长为
，S1的面积为
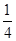x2，
∴S1，S2的比值为9:8，
故选C．
如图，设正方形的边长为x，
根据等腰直角三角形的性质知，AC=
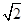BC，BC=CE=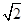CD，∴AC=2CD，CD=
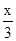，∴S2的边长为
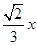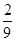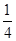，S2的面积为x2，S1的边长为，S1的面积为x2，∴S1，S2的比值为9:8，
故选C．
练习册系列答案
相关题目
BD，E、F、G、H分别为AB、BC、CD、DA的中点.
