题目内容
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)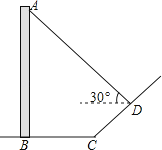
【答案】解: 延长AD交BC的延长线于E,作DF⊥BE于F,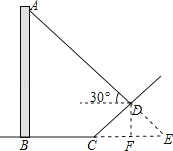
∵∠BCD=150°,
∴∠DCF=30°,又CD=4,
∴DF=2,CF= ![]() =2
=2 ![]() ,
,
由题意得∠E=30°,
∴EF= ![]() =2
=2 ![]() ,
,
∴BE=BC+CF+EF=6+4 ![]() ,
,
∴AB=BE×tanE=(6+4 ![]() )×
)× ![]() =(2
=(2 ![]() +4)米,
+4)米,
答:电线杆的高度为(2 ![]() +4)米
+4)米
【解析】延长AD交BC的延长线于E,作DF⊥BE于F,根据直角三角形的性质和勾股定理求出DF、CF的长,根据正切的定义求出EF,得到BE的长,根据正切的定义解答即可.本题考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
【考点精析】认真审题,首先需要了解关于仰角俯角问题(仰角:视线在水平线上方的角;俯角:视线在水平线下方的角).

【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一
a | b | c |
3 | 4 | 5 |
5 | 12 | 13 |
7 | 24 | 25 |
9 | 41 |
表二
a | b | c |
6 | 8 | 10 |
8 | 15 | 17 |
10 | 24 | 26 |
12 | 41 |
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是 ,a、b、c之间的数量关系是 ;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是 ,a、b、c之间的数量关系是 ;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当![]() ,b=
,b= 时,斜边c的值.
时,斜边c的值.