题目内容
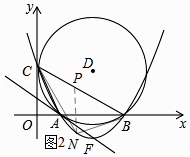
【题目】如图1,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.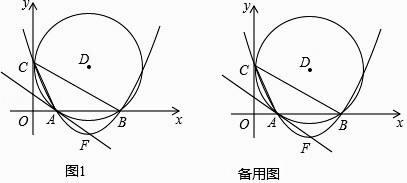
(1)D点的坐标是 , 圆的半径为;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大面积是多少?并求出N点坐标.
【答案】
(1)(5,4);5
(2)
解:如图1所示:
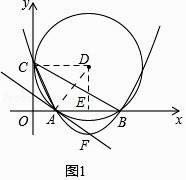
∵D(5,4),
∴E(5,0).
∴A(2,0)、B(8,0).
设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入得:16a=4,解得:a= ![]() ,
,
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+4.
x+4.
(3)
解:∵y= ![]() x2﹣
x2﹣ ![]() x+4,
x+4,
∴抛物线的顶点坐标F(5,﹣ ![]() ).
).
∴DF=4+ ![]() =
= ![]() ,AF=
,AF= ![]() =
= ![]() .
.
又∵AD=5.
∴AD2+AF2=DF2,
∴△DAF为直角三角形.
∴∠DAF=90°.
∴AF是⊙D的切线.
(4)
解:如图2所示:过点N作NP∥y轴,交BC与点P.
设BC的解析式为y=kx+4,将点B的坐标代入得:8k+4=0,解得k=﹣ ![]() .
.
∴BC的解析式为y=﹣ ![]() x+4.
x+4.
设N点坐标(a, ![]() a2﹣
a2﹣ ![]() a+4),则点P坐标为(a,﹣
a+4),则点P坐标为(a,﹣ ![]() a+4).
a+4).
∴NP=﹣ ![]() a+4﹣(
a+4﹣( ![]() a2﹣
a2﹣ ![]() a+4)=﹣
a+4)=﹣ ![]() a2+2a.
a2+2a.
∴S△ABC=S△CPN+S△PBN= ![]() ×BO×PN=
×BO×PN= ![]() ×8×(﹣
×8×(﹣ ![]() a2+2a)=﹣(a﹣4)2+16.
a2+2a)=﹣(a﹣4)2+16.
∴当a=4时,S△ABC最大,最大值为16,此时,N(4,﹣2).
【解析】解:(1)连接CD,过点D作DE⊥AB,垂足为E,连接AD.
∵DE⊥AB,
∴AE= ![]() AB=3.
AB=3.
∵⊙D与y轴相切,
∴DC⊥y轴.
∵∠COE=∠OED=∠OCD=90°,
∴四边形OCDE为矩形.
∴OC=DE.
∵C(0,4),
∴DE=4.
在Rt△AED中,AD= ![]() =5.
=5.
∴⊙D的半径为5.
∴D(5,4).
所以答案是:(5,4),5.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案【题目】某中学七年级四班的同学在体检中测量了自己的身高,并求出了该班同学的平均身高.
(1)下表给出了该班5名同学的身高情况(单位:cm),试完成该表,并求出该班同学的平均身高.
姓名 | 刘杰 | 刘涛 | 李明 | 张春 | 刘建 |
身高 | 161 |
|
| 165 | 155 |
身高与全班同 学平均身高差 | +3 | ﹣1 | 0 |
|
|
(2)谁最高?谁最矮?
(3)计算这5名同学的平均身高是多少?