题目内容
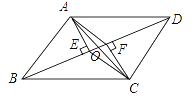
【题目】如图在平行四边形ABCD中,AC交BD于点O,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:四边形AECF为平行四边形.
【答案】证明见解析.
【解析】试题分析:由四边形ABCD是平行四边形,可得AB=CD,AB∥CD,又由AE⊥BD,CF⊥BD,即可得AE∥CF,∠AEB=∠CFD=90°,然后利用AAS证得△AEB≌△CFD,即可得AE=CF,由有一组对边相等且平行的四边形是平行四边形,即可证得四边形AECF是平行四边形.
试题解析:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△AEB和△CFD中,
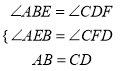 ,
,
∴△AEB≌△CFD(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】大学生小李自主创业,春节期间购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
要使销售文具所获利润不超过进货价格的40%,求至少要购进多少只A型文具?