Question

如图，在四边形中，，，，已知四边形的周长为32，求的长.

 

 

Answer 1

【答案】

10

【解析】

试题分析：连结BD，由AB=AD=8，∠A=60°可证得△ABD为等边三角形，即得BD=8，∠ADB=60°，再结合∠ADC=150°可得∠CDB=90°，根据四边形的周长为32可得BC+CD=16，设BC=x，则CD=16-x，在Rt△DBC中，由勾股定理即可列方程求解.

解：连结BD

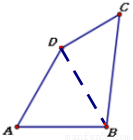
∵AB=AD=8，∠A=60°，

∴△ABD为等边三角形

∴BD=8，∠ADB=60°

∵∠ADC=150°，

∴∠CDB=90°

∵C_{四边形ABCD}=AB+BC+CD+DA=32

∴BC+CD=16

设BC=x，则CD=16-x

在Rt△DBC中，由勾股定理可得：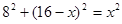

解得x=10，即BC=10.

考点：等边三角形的判定和性质，勾股定理

点评：勾股定理是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.