题目内容
如图,在四边形 中,点
中,点 ,
, 分别是
分别是 的中点,
的中点, 分别是
分别是 的中点,
的中点, 满足什么条件时,四边形
满足什么条件时,四边形 是菱形?请证明你的结论.
是菱形?请证明你的结论.

【答案】
当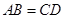 时,四边形
时,四边形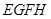 是菱形。证明见解析
是菱形。证明见解析
【解析】(1)当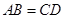 时,四边形
时,四边形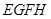 是菱形.·············· 1分
是菱形.·············· 1分
(2)证明: 点
点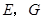 分别是
分别是 的中点,
的中点,
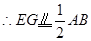 ,同理
,同理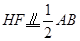 ,
,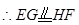 .
.
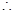 四边形
四边形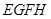 是平行四边形························ 6分
是平行四边形························ 6分
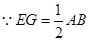 ,又可同理证得
,又可同理证得 ,
,
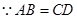 ,
,
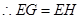 ,
,
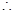 四边形
四边形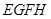 是菱形.·························· 9分
是菱形.·························· 9分
(用分析法由四边形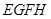 是菱形推出满足条件“
是菱形推出满足条件“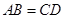 ”也对)
”也对)
根据菱形的定义来求解.E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥=HF.
因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH= 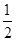 CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件

练习册系列答案
相关题目
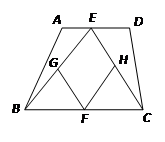
 中,点
中,点 是线段
是线段 上的任意一点(
上的任意一点( 不重合),
不重合),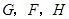 分别是
分别是 的中点.
的中点.
 的形状并说明理由;
的形状并说明理由; ,且
,且 ,证明平行四边形
,证明平行四边形 中,点
中,点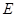 ,
,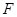 分别是
分别是 的中点,
的中点,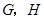 分别是
分别是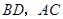 的中点,
的中点,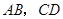 满足什么条件时,四边形
满足什么条件时,四边形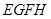 是菱形?请证明你的结论.
是菱形?请证明你的结论.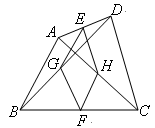
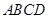 中,点
中,点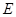 是线段
是线段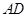 上的任意一点(
上的任意一点(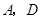 不重合),
不重合), 分别是
分别是 的中点.
的中点.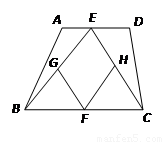
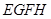 的形状并说明理由;
的形状并说明理由;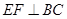 ,且
,且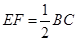 ,证明平行四边形
,证明平行四边形