Question

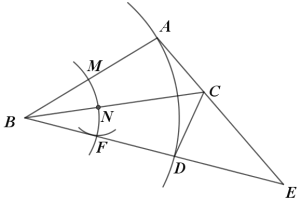
【题目】饮料厂生产某品牌的饮料成本是每瓶5元，每天的生产量不超过9000瓶．根据市场调查，以单价8元批发给经销商，经销商每天愿意经销5000瓶，并且表示单价每降价0.1元，经销商每天愿意多经销500瓶．

（1）求出饮料厂每天的利润（元）与批发单价（元）之间的函数关系式；

（2）批发单价定为多少元时，饮料厂每天的利润最大，最大利润是多少元；

（3）如果该饮料厂要使每天的利润不低于18750元，且每天的总成本不超过42500元，那么批发单价应控制在什么范围．（每天的总成本每瓶的成本每天的经销量）

Answer 1

【答案】（1）；（2）当批发单价为7.2元时，饮料厂每天的利润最大，最大利润是19800元；（3）批发单价应控制在7.3元到7.5元之间．

【解析】

（1）根据每天利润=单价×每日销售量列函数关系式求解；

（2）由每天的生产量不超过9000瓶，列不等式求得x的取值范围，然后结合二次函数的性质分析最值；

（3）当y=18750时，求得对应的x的值，然后结合二次函数性质确定x的取值范围，再根据每天的总成本不超过42500元，列不等式求x的取值范围，最后确定解集，从而求解．

解：（1）根据题意，得：

答：与的函数关系式为

（2）由题意，得

解得

∵，

∴抛物线开口向下，对称轴为直线

∵

∴此时函数图象在对称轴的右侧，随的增大而减小

∴时，取得最大值，

答：当批发单价为7.2元时，饮料厂每天的利润最大，最大利润是19800元

（3）根据题意得

解得：，

∵抛物线开口向下，

∴当时，每天的利润不低于18700元

∵每天的总成本不超过42500元

∴

解得

∴

答：批发单价应控制在7.3元到7.5元之间．