题目内容
【题目】探究题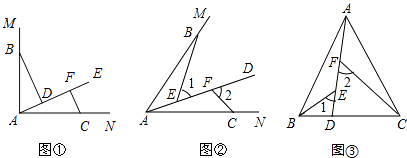
(1)理解证明:
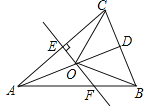
如图1,∠MAN=90°,射线AE在这个角的内部,点B,C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明△ABD≌△CAF;
(2)类比探究:
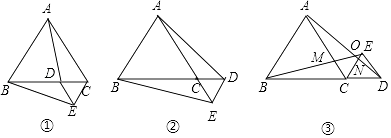
如图2,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为多少?
【答案】
(1)
证明:∵CF⊥AE,BD⊥AE,
∴∠ADB=∠CFA=90°,
∵∠MAN=90°,
∴∠ABD+∠BAD=90°,又∠CAF+∠BAD=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
 ,
,
∴△ABD≌△CAF;
(2)
证明:∵∠1=∠2,
∴∠ABE=∠CAF,
∵∠1=∠ABE+∠EAB,∠1=∠BAC,
∴∠ABE=∠CAF,
在△ABE和△CAF中,
 ,
,
∴△ABE≌△CAF;
(3)
∵△ABC的面积为15,CD=2BD,
∴△ABD的面积为15× ![]() =5,
=5,
由类比探究得,△ABE≌△CAF,
∴△ACF与△BDE的面积之和=△ABD的面积=5
【解析】理解证明:根据AAS证明△ABD≌△CAF;
类比探究:根据AAS证明即可;
拓展应用:利用类比探究的结论、三角形的面积公式计算即可.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目