题目内容
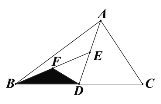
【题目】如图，已知△ABC，求作一点P，使P到∠A的两边的距离相等，且PA＝PB、下列确定P点的方法正确的是（ ）
A.P为∠A、∠B两角平分线的交点
B.P为AC、AB两边上的高的交点
C.P为∠A的角平分线与AB的垂直平分线的交点
D.P为AC、AB两边的垂直平分线的交点
【答案】C
【解析】
首先根据P到∠A的两边的距离相等，应用角平分线的性质，可得点P在∠A的角平分线上；然后根据PA=PB，应用线段垂直平分线的性质，可得点P在AB的垂直平分线上，所以P为∠A的角平分线与AB的垂直平分线的交点，据此判断即可．
解：∵P到∠A的两边的距离相等，
∴点P在∠A的角平分线上
∵PA＝PB，
∴点P在AB的垂直平分线上
∴P为∠A的角平分线与AB的垂直平分线的交点．
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
