题目内容
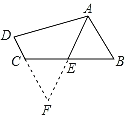
【题目】如图，在四边形ABCD中，AB∥CD，点E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系．解决此问题可以用如下方法：延长AE交DC的延长线于点F，从而把AB，AD，DC转化在一个三角形中即可判断．试探究AB，AD，DC之间的等量关系，并证明你的结论．
【答案】AD＝AB+DC；证明见解析
【解析】
延长AE交DC的延长线于点F，证明△AEB≌△FEC，根据全等三角形的性质得到AB=FC，根据等腰三角形的判定得到DF=AD，证明结论．
解：AD＝AB+DC；
理由如下：延长AE交DC的延长线于点F，
∵AB∥DC，
∴∠BAF＝∠F，
∵E是BC的中点，
∴CE＝BE，
在△AEB和△FEC中，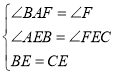
，
∴△AEB≌△FEC（AAS），
∴AB＝FC，
∵AE是∠BAD的平分线，
∴∠DAF＝∠BAF，
∴∠DAF＝∠F，
∴DF＝AD，
∴AD＝DC+CF＝DC+AB，
即AD＝AB+DC
练习册系列答案
新思维寒假作业系列答案
相关题目
