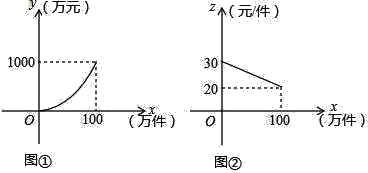
��Ŀ����
����Ŀ���������龳����ͼ�٣��ڡ�ABC�У���AB=10��AC=6����BC���ϵ�����AD��ȡֵ��Χ��
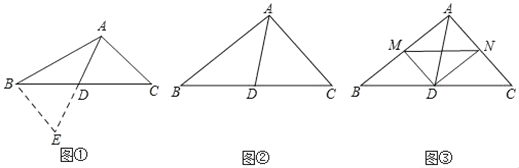
��1�������������ӳ�AD����EʹDE=AD��������BE����ACD���ŵ�D��ʱ����ת180���õ���EBD������AB��AC��2AD�����ڡ�ABE�У��������������ߵĹ�ϵ�����жϳ�����AD��ȡֵ��Χ���� ����
����˼������ʱ�����������������е����������������������Կ��ǹ����Ը��е�Ϊ�Գ����ĵ����ĶԳ�ͼ�Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��е�ͬ���������У��Ӷ�������⣮
��2��������Ӧ�ã���ͼ�ڣ���ABC�У���BAC=90����AD��BC���ϵ����ߣ��Բ����߶�AB��AC��AD֮���������ϵ����˵�����ɣ�
��3������չ���죩��ͼ�ۣ���ABC�У���BAC=90����D��BC���е㣬DM��DN��DM��AB�ڵ�M��DN��AC�ڵ�N������MN����BM=4��MN=5��AC=6ʱ����ֱ��д������AD�ij���
���𰸡���1��2��AD��8����2��AB2��AC2��4AD2�����ɼ���������3��AD��5��
��������
��1���ӳ�AD��E��ʹDE��AD����SAS֤����BDE�ա�CDA���ó�BE��AC��8������ABE�У��������ε����߹�ϵ���AE��ȡֵ��Χ�����ɵó�AD��ȡֵ��Χ��
��2���ӳ�AD��E��ʹDE��AD������BE����ͼ����ʾ���ɣ�1����֪��BDE�ա�CDA��Ȼ��ֻҪ֤����ABE��90�������ù��ɶ������ɵó����ۣ�
��3���ӳ�ND��E��ʹ��DN��DE������BE��EM������֤����BDE�ա�CDN�������ABD����DBE��90����Ȼ�����ù��ɶ����ɵ�BE��3�������õ�AN��NC���������ߺ�һ֤��DN��AC��ͬ���ɵ�DM��AB��Ȼ��֤���ı���AMDN�Ǿ��μ��ɽ������.
�⣺��1���ӳ�AD��E��ʹDE��AD������BE����ͼ����ʾ��
��AD��BC���ϵ����ߣ�
��BD��CD��
����BDE����CDA��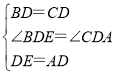 ��
��
���BDE�ա�CDA��SAS����
��BE��AC��6��
����ABE�У��������ε����߹�ϵ�ã�ABBE��AE��AB��BE��
��106��AE��10��6����4��AE��16��
��2��AD��8��
��2��AB2��AC2��4AD2��
���ɣ��ӳ�AD��E��ʹDE��AD������BE����ͼ����ʾ��
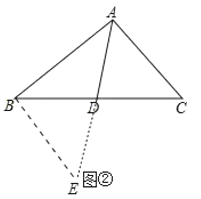
�ɣ�1����֪����BDE�ա�CDA��
��BE��AC����E����CAD��
�ߡ�BAC��90����
���E����BAE����BAE����CAD����BAC��90����
���ABE��90����
��AB2��BE2��AE2��
��AB2��AC2��4AD2��
��3����ͼ�ۣ��ӳ�ND��E��ʹ��DN��DE������BE��EM��
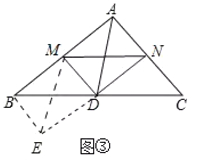
��BD��DC����BDE����CDN��DE��DN��
���BDE�ա�CDN��
��BE��CM����EBD����C��
�ߡ�ABC����C��90����
���ABD����DBE��90����
��MD��EN��DE��DN��
��ME��MN��5��
��Rt��BEM��BE��![]() ��3��
��3��
��CN��BE��3��
��AC��6��
��AN��NC��
�ߡ�BAC��90����BD��DC��
��AD��DC��BD��
��DN��AC��
��Rt��AMN��AM��![]() ��4��
��4��
��AM��BM��
��DA��DB��
��DM��
���AMD����AND����MAN��90����
���ı���AMDN�Ǿ��Σ�
��AD��MN��5��