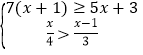题目内容
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3…,按此作法进行下去,则
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3…,按此作法进行下去,则![]() 的长为______(用含n,π的式子表示).
的长为______(用含n,π的式子表示).

【答案】![]()
【解析】
依据直线l为![]() ,点A1(1,0),A1B1⊥x轴,可得A2(2,0),同理可得,A3(4,0),A4(8,0),…,依据规律可得点An的坐标为(2n-1,0),可得OBn-1的长,由弧长公式可求解.
,点A1(1,0),A1B1⊥x轴,可得A2(2,0),同理可得,A3(4,0),A4(8,0),…,依据规律可得点An的坐标为(2n-1,0),可得OBn-1的长,由弧长公式可求解.
∵直线l为![]() ,点A1(1,0),A1B1⊥x轴,
,点A1(1,0),A1B1⊥x轴,
∴当x=1时,y=![]() ,
,
即B1(1,![]() ),
),
∴tan∠A1OB1=![]() ,
,
∴∠A1OB1=60°,∠A1B1O=30°,
∴OB1=2OA1=2,
∵以原点O为圆心,OB1长为半径画圆弧交x轴于点A2,
∴A2(2,0),
同理可得,A3(4,0),A4(8,0),…,
∴点An的坐标为(2n-1,0),
∴OAn=2n-1,
∴OBn-1=2×2n-1=2n,
∴弧![]() =
=![]()
故答案为:![]()

练习册系列答案
相关题目