题目内容
(1997•昆明)已知方程2x2+(a+2)x-2a+1=0,求当a是什么值时,两根的平方和等于3
?
| 1 | 4 |
分析:设方程两个为x1,x2,根据根与系数的关系得到x1+x2=-
,x1•x2=
,由于x12+x22=(x1+x2)2-2x1•x2=
,则(-
)2-2×
=
,解方程得a1=-13,a2=1,再分别把a的值代入方程求对应的判别式,然后根据判别式的意义确定满足条件的a的值.
| a+2 |
| 2 |
| -2a+1 |
| 2 |
| 13 |
| 4 |
| a+2 |
| 2 |
| -2a+1 |
| 2 |
| 13 |
| 4 |
解答:解:设方程两个为x1,x2,则x1+x2=-
,x1•x2=
,
∵x12+x22=(x1+x2)2-2x1•x2=
,
∴(-
)2-2×
=
,
整理得a2+12a-13=0,解得a1=-13,a2=1,
当a=-13时,原方程化为2x2-11x+27=0,△=112-4×2×27<0,方程无实数根,所以a=-13舍去;
当a=1时,原方程化为2x2+3x-1=0,△=9-4×2×(-1)>0,
故当a是1时,两根的平方和等于3
.
| a+2 |
| 2 |
| -2a+1 |
| 2 |
∵x12+x22=(x1+x2)2-2x1•x2=
| 13 |
| 4 |
∴(-
| a+2 |
| 2 |
| -2a+1 |
| 2 |
| 13 |
| 4 |
整理得a2+12a-13=0,解得a1=-13,a2=1,
当a=-13时,原方程化为2x2-11x+27=0,△=112-4×2×27<0,方程无实数根,所以a=-13舍去;
当a=1时,原方程化为2x2+3x-1=0,△=9-4×2×(-1)>0,
故当a是1时,两根的平方和等于3
| 1 |
| 4 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
,x1•x2=
.也考查了一元二次方程根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
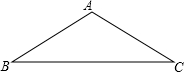 (1997•昆明)已知等腰三角形ABC的顶角A为120°,底边长为20cm,求腰长.
(1997•昆明)已知等腰三角形ABC的顶角A为120°,底边长为20cm,求腰长.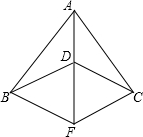 (1997•昆明)已知:如图,AB=AC,DB=DC,F是AD的延长线上一点.求证:BF=CF.
(1997•昆明)已知:如图,AB=AC,DB=DC,F是AD的延长线上一点.求证:BF=CF. (1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.
(1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.