题目内容
 (1997•昆明)已知等腰三角形ABC的顶角A为120°,底边长为20cm,求腰长.
(1997•昆明)已知等腰三角形ABC的顶角A为120°,底边长为20cm,求腰长.分析:先求出底角等于30°,再根据30°的直角三角形的性质求解.
解答: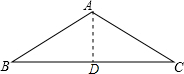 解:作AD⊥BC于D.
解:作AD⊥BC于D.
∵∠BAC=120°,AB=AC,
∴底边上的高AD,即中线AD,∠B=
(180°-120°)=30°.
∵底边长为20cm,
∴BD=10cm,
∴AD=
AB.(直角三角形中30°所对直角边等于斜边的一半),
∴AB2-(
AB)2=102,
解得AB=
.
答:腰长为
.
 解:作AD⊥BC于D.
解:作AD⊥BC于D.∵∠BAC=120°,AB=AC,
∴底边上的高AD,即中线AD,∠B=
| 1 |
| 2 |
∵底边长为20cm,
∴BD=10cm,
∴AD=
| 1 |
| 2 |
∴AB2-(
| 1 |
| 2 |
解得AB=
20
| ||
| 3 |
答:腰长为
20
| ||
| 3 |
点评:本题考查了等腰三角形的三线合一性质和含30°角的直角三角形的性质.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
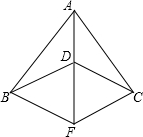 (1997•昆明)已知:如图,AB=AC,DB=DC,F是AD的延长线上一点.求证:BF=CF.
(1997•昆明)已知:如图,AB=AC,DB=DC,F是AD的延长线上一点.求证:BF=CF. (1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.
(1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.