题目内容
【题目】(1)如图1,4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线的距离都是2cm,正方形ABCD的4个顶点A、B、C、D分别在l1、l3、l4、l2上,求该正方形的面积;
(2)如图2,把一张矩形卡片ABCD放在每格宽度为18mm的横格纸中,恰好四个顶点都在横格线上,已知∠1=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)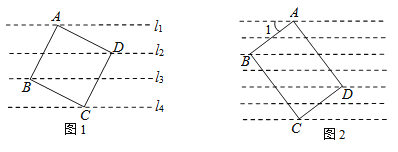
【答案】解:(1)如图1,作EF⊥l2 , 交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4 , EF⊥l2 ,
∴EF⊥l1 , EF⊥l4 ,
即∠AED=∠DFC=90°.
∵四边形ABCD为正方形,
∴∠ADC=90°.
∴∠ADE+∠CDF=90°.
又∵∠ADE+∠DAE=90°,
∴∠CDF=∠DAE.
∵AD=CD,
在△ADE和△DCF,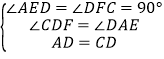 ,
,
∴△ADE≌△DCF(AAS),
∴CF=DE=2.
∵DF=4,
∴CD2=22+42=20,
即正方形ABCD的面积为20cm2;
(2)如图2,作BE⊥l于点E,DF⊥l于点F.
∵∠1+∠DAF=180°﹣∠BAD=180°﹣90°=90°,∠ADF+∠DAF=90°,
∴∠ADF=∠1=36°,
根据题意,得BE=36mm,DF=72mm.
在Rt△ABE中,sin∠1=![]() ,
,
∴AB=![]() =60mm,
=60mm,
在Rt△ADF中,cos∠ADF=![]() ,
,
∴AD=![]() mm=90mm.
mm=90mm.
∴矩形ABCD的周长=2(60+90)=300mm.
【解析】(1)过D点作直线EF与平行线垂直,与l1交于点E,与l4交于点F.易证△ADE≌△DFC,得CF=2,DF=4.根据勾股定理可求CD2得正方形的面积;
(2)作BE⊥l于点E,DF⊥l于点F,求∠ADF的度数,在Rt△ABE中,可以求得AB的值,在Rt△ADF中,可以求得AD的值,即可计算矩形ABCD的周长,即可解题.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


