题目内容
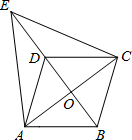 (2012•朝阳区一模)如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形,若AC=8,AB=5,求ED的长.
(2012•朝阳区一模)如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形,若AC=8,AB=5,求ED的长.分析:根据平行四边形的对角线互相平分可得AO=CO,BO=DO,再根据△EAC是等边三角形可以判定EO⊥AC,并求出EA的长度,然后在Rt△ABO中,利用勾股定理列式求出BO的长度,即DO的长度,在Rt△AOE中,根据勾股定理列式求出EO的长度,再根据ED=EO-DO计算即可得解.
解答:解:∵四边形ABCD是平行四边形,
∴AO=CO=
AC=
×8=4,DO=BO,
∵△EAC是等边三角形,
∴EA=AC=8,EO⊥AC,…(2分)
在Rt△ABO中,BO=
=
=3,
∴DO=BO=3,…(3分)
在Rt△EAO中,EO=
=
=4
.…(4分)
∴ED=EO-DO=4
-3.…(5分)
∴AO=CO=
| 1 |
| 2 |
| 1 |
| 2 |
∵△EAC是等边三角形,
∴EA=AC=8,EO⊥AC,…(2分)
在Rt△ABO中,BO=
| AB2-AO2 |
| 52-42 |
∴DO=BO=3,…(3分)
在Rt△EAO中,EO=
| EA2-AO2 |
| 82-42 |
| 3 |
∴ED=EO-DO=4
| 3 |
点评:本题考查了平行四边形对角线互相垂直平分的性质,等边三角形的性质,以及勾股定理的应用,根据等边三角形三线合一的性质判断出EO⊥AC是解题的关键,也是本题的难点.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 (2012•朝阳区一模)在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
(2012•朝阳区一模)在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
 (2012•朝阳区一模)如图,P是反比例函数
(2012•朝阳区一模)如图,P是反比例函数