题目内容
 (2012•朝阳区一模)在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
(2012•朝阳区一模)在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.(1)求此抛物线的解析式;
(2)点P(x,y)为此抛物线上一动点,连接MP交此抛物线的对称轴于点D,当△DMN为直角三角形时,求点P的坐标;
(3)设此抛物线与y轴交于点C,在此抛物线上是否存在点Q,使∠QMN=∠CNM?若存在,求出点Q的坐标;若不存在,说明理由.
分析:(1)根据MN平行x轴,MN=6,点N坐标为(2,-5),可得出点M的坐标,然后利用待定系数法求解函数解析式即可;
(2)设抛物线的对称轴x=-1交MN于点G,此时抛物线的对称轴是MN的中垂线,根据△DMN为直角三角形,可得出D1及D2的坐标,分别求出MD1及MD2的函数解析式,结合抛物线可得出点P的坐标;
(3)分两种情况进行讨论,①点Q在MN上方,②点Q在MN下方,然后根据两角相等,利用三角函数建立方程,解出x的值后检验即可得出答案.
(2)设抛物线的对称轴x=-1交MN于点G,此时抛物线的对称轴是MN的中垂线,根据△DMN为直角三角形,可得出D1及D2的坐标,分别求出MD1及MD2的函数解析式,结合抛物线可得出点P的坐标;
(3)分两种情况进行讨论,①点Q在MN上方,②点Q在MN下方,然后根据两角相等,利用三角函数建立方程,解出x的值后检验即可得出答案.
解答:解:(1)由题意得,MN平行x轴,MN=6,点N坐标为(2,-5),
故可得点M坐标为(-4,-5),
∵y=ax2+bx+3过点M(-4,-5)、N(2,-5),
∴可得
,
解得:
,
故此抛物线的解析式为y=-x2-2x+3.
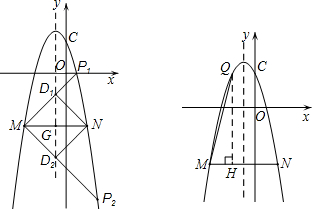
(2)设抛物线的对称轴x=-1交MN于点G,
若△DMN为直角三角形,则GD1=GD2=
MN=3,
可得D1(-1,-2),D2(-1,-8),
从而可求得直线MD1解析式为;y=x-1,直线MD2解析式为:y=-x-9,
将P(x,-x2-2x+3)分别代入直线MD1,MD2的解析式,
得-x2-2x+3=x-1①,-x2-2x+3=-x-9②、
解①得 x1=1,x2=-4(舍),
即P1(1,0);
解②得 x3=3,x4=-4(舍),
即P2(3,-12);
故当△DMN为直角三角形时,点P的坐标为(1,0)或(3,-12).
(3)设存在点Q(x,-x2-2x+3),使得∠QMN=∠CNM,
①若点Q在MN上方,过点Q作QH⊥MN,交MN于点H,
则QH=-x2-2x+3+5,MH=(x+4)、
故
=tan∠CNM=4,即-x2-2x+3+5=4(x+4)、
解得x1=-2,x2=-4(舍),
故可得点Q1(-2,3);
②若点Q在MN下方,
同理可得Q2(6,-45).
综上可得存在点Q,使∠QMN=∠CNM,点Q的坐标为(-2,3)或(6,-45).
故可得点M坐标为(-4,-5),
∵y=ax2+bx+3过点M(-4,-5)、N(2,-5),
∴可得
|
解得:
|
故此抛物线的解析式为y=-x2-2x+3.

(2)设抛物线的对称轴x=-1交MN于点G,
若△DMN为直角三角形,则GD1=GD2=
| 1 |
| 2 |
可得D1(-1,-2),D2(-1,-8),
从而可求得直线MD1解析式为;y=x-1,直线MD2解析式为:y=-x-9,
将P(x,-x2-2x+3)分别代入直线MD1,MD2的解析式,
得-x2-2x+3=x-1①,-x2-2x+3=-x-9②、
解①得 x1=1,x2=-4(舍),
即P1(1,0);
解②得 x3=3,x4=-4(舍),
即P2(3,-12);
故当△DMN为直角三角形时,点P的坐标为(1,0)或(3,-12).
(3)设存在点Q(x,-x2-2x+3),使得∠QMN=∠CNM,
①若点Q在MN上方,过点Q作QH⊥MN,交MN于点H,
则QH=-x2-2x+3+5,MH=(x+4)、
故
| QH |
| MH |
解得x1=-2,x2=-4(舍),
故可得点Q1(-2,3);
②若点Q在MN下方,
同理可得Q2(6,-45).
综上可得存在点Q,使∠QMN=∠CNM,点Q的坐标为(-2,3)或(6,-45).
点评:此题属于二次函数的综合题,涉及了待定系数法求函数解析式、一元二次方程的求解及三角函数的知识,难点在第二问和第三问,注意要分类讨论,不要漏解,要求我们能将所学的知识融会贯通.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 (2012•朝阳区一模)如图,P是反比例函数
(2012•朝阳区一模)如图,P是反比例函数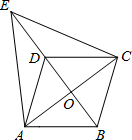 (2012•朝阳区一模)如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形,若AC=8,AB=5,求ED的长.
(2012•朝阳区一模)如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形,若AC=8,AB=5,求ED的长.