题目内容
一个多边形除去一个内角后,其余各内角的和为2210°,则该多边形的边数是
- A.13
- B.14
- C.15
- D.16
C
分析:n边形的内角和是(n-2)•180°,因而内角和一定是180度的整数倍,即可求解.
解答:∵n边形的内角和是(n-2)•180°,
∴2210÷180=12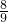 ,则正多边形的边数是:13+2=15边形.
,则正多边形的边数是:13+2=15边形.
故选C.
点评:本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
分析:n边形的内角和是(n-2)•180°,因而内角和一定是180度的整数倍,即可求解.
解答:∵n边形的内角和是(n-2)•180°,
∴2210÷180=12
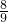 ,则正多边形的边数是:13+2=15边形.
,则正多边形的边数是:13+2=15边形.故选C.
点评:本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.

练习册系列答案
相关题目
一个多边形除去一个内角后,其余各内角的和为2210°,则该多边形的边数是( )
| A、13 | B、14 | C、15 | D、16 |