题目内容
【题目】如图,CD是圆O的弦,AB是直径,且CD⊥AB,垂足为P.
(1)求证:PC2=PAPB;
(2)PA=6,PC=3,求圆O的直径.

【答案】(1)证明见解析;(2)7.5.
【解析】
试题分析:(1)连接AC、BC,结合条件和垂径定理可证明△APC∽△CPB,利用相似三角形的性质可证得PC2=PAPB;
(2)把PA、PC的长代入(1)中的结论,可求得PB,则可求得AB的长.
试题解析:(1)证明:如图,连接AC、BC,∵CD⊥AB,AB是直径,∴![]() ,∴∠CAB=∠BCP,∵∠CPA=∠CPB=90°,∴△APC∽△CPB,∴
,∴∠CAB=∠BCP,∵∠CPA=∠CPB=90°,∴△APC∽△CPB,∴![]() ,即PC2=PAPB;
,即PC2=PAPB;
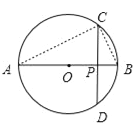
(2)将PA=6,PC=3,代入PC2=PAPB,可得32=6PB,∴PB=1.5,∴AB=PA+PB=6+1.5=7.5,即圆的直径为7.5.

练习册系列答案
相关题目