题目内容
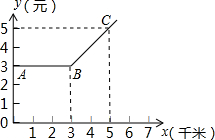 如图所示的折线ABC为某地出租汽车收费y(元)与乘坐路程x(千米)之间的函数关系式图象,当x≥3千米时,该函数的解析式为
如图所示的折线ABC为某地出租汽车收费y(元)与乘坐路程x(千米)之间的函数关系式图象,当x≥3千米时,该函数的解析式为分析:观察图象可设当x≥3千米时,该函数的解析式为y=kx+b,由点B(3,3)与点C(5,5)在其函数图象上,利用待定系数法即可求得该函数的解析式;观察图象即可求得乘坐2千米时的车费,将x=8代入所求函数,即可求得乘坐8千米时的车费.
解答:解:设当x≥3千米时,该函数的解析式为y=kx+b,
∵点B(3,3)与点C(5,5)在其函数图象上,
∴
,
解得:
,
∴当x≥3千米时,该函数的解析式为:y=x;
观察图象可得:坐2千米时,车费为3元,
当x=8时,y=x=8,
∴乘坐8千米时,车费为8元.
故答案为:y=x,3,8.
∵点B(3,3)与点C(5,5)在其函数图象上,
∴
|
解得:
|
∴当x≥3千米时,该函数的解析式为:y=x;
观察图象可得:坐2千米时,车费为3元,
当x=8时,y=x=8,
∴乘坐8千米时,车费为8元.
故答案为:y=x,3,8.
点评:此题考查了一次函数的应用问题.题目比较简单,解题的关键是仔细观察图象,根据图象解题,注意待定系数法的应用.

练习册系列答案
相关题目
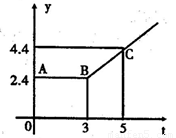
 如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.