题目内容
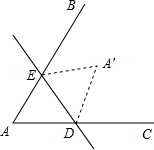
 一张三角形纸片部分如图所示,将∠A折叠,ED为折痕,A点落在A'位置,若∠A=70°,则∠A′EB+∠A′DC=( )
一张三角形纸片部分如图所示,将∠A折叠,ED为折痕,A点落在A'位置,若∠A=70°,则∠A′EB+∠A′DC=( )分析:利用翻折变换的性质得出,∠A=∠A′=70°,再利用四边形内角和定理求出∠A′+∠A+∠AEA′+∠ADA′=360°,再利用邻补角的性质求出∠A′+∠A+∠AEA′+∠ADA′=360°,即可得出答案.
解答:解:∵将∠A折叠,ED为折痕,A点落在A'位置,∠A=70°,
∴∠A′=70°,
∵在四边形ADA′E中,
∴∠A′+∠A+∠AEA′+∠ADA′=360°,
∵∠AEA′+∠ADA′+∠A′EB+∠A′DC=360°,
∴∠A′EB+∠A′DC=∠A+∠A′=140°,
故选:A.
∴∠A′=70°,
∵在四边形ADA′E中,
∴∠A′+∠A+∠AEA′+∠ADA′=360°,
∵∠AEA′+∠ADA′+∠A′EB+∠A′DC=360°,
∴∠A′EB+∠A′DC=∠A+∠A′=140°,
故选:A.
点评:此题主要考查了四边形内角和定理以及邻补角的性质,利用已知得出∠A′+∠A+∠AEA′+∠ADA′=360°,∠A′+∠A+∠AEA′+∠ADA′=360°是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

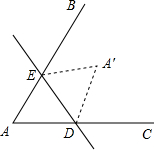 一张三角形纸片部分如图所示,将∠A折叠,ED为折痕,A点落在A'位置,若∠A=70°,则∠A′EB+∠A′DC=
一张三角形纸片部分如图所示,将∠A折叠,ED为折痕,A点落在A'位置,若∠A=70°,则∠A′EB+∠A′DC=