题目内容
将量角器按如右图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为86°、30°，则∠ACB的大小为
A．15
B．28 C．29 D．34
A．15
B．28 C．29 D．34B
首先设半圆圆心为O，连OA，OB，由点A、B 的读数分别为86°、30°，即可求得∠AOB的度数，又由圆周角定理，即可求得∠ACB的大小．
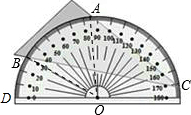
解：设半圆圆心为O，连OA，OB，如图：
∵点A、B 的读数分别为86°、30°，
∴∠BOD=30°，∠AOD=86°，
∴∠AOB=∠AOD-∠BOD=86°-30°=56°，
∵∠ACB=
∠AOB，
∴∠ACB=×56°=28°．
故答案为：28°．
本题考查了圆周角定理．解题的关键是注意掌握：在同圆或等圆中，同弧和等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．注意辅助线的作法．
解：设半圆圆心为O，连OA，OB，如图：
∵点A、B 的读数分别为86°、30°，
∴∠BOD=30°，∠AOD=86°，
∴∠AOB=∠AOD-∠BOD=86°-30°=56°，
∵∠ACB=
∠AOB，∴∠ACB=
×56°=28°．故答案为：28°．
本题考查了圆周角定理．解题的关键是注意掌握：在同圆或等圆中，同弧和等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．注意辅助线的作法．
练习册系列答案
相关题目
，△ABC是 【 】
．
