题目内容
【题目】如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以1cm/s的速度沿FG方向移动,移动开始前点A与点F重合,在移动过程中,边AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为1cm,矩形EFGH的边FG,GH的长分别为4cm,3cm,设正方形移动时间为x(s),线段GP的长为y(cm),其中0≤x≤2.5. 
(1)试求出y关于x的函数关系式,并求当y=3时相应x的值;
(2)记△DGP的面积为S1 , △CDG的面积为S2 . 试说明S1﹣S2是常数;
(3)当线段PD所在直线与正方形ABCD的对角线AC垂直时,求线段PD的长.
【答案】
(1)解:∵CG∥AP,
∴∠CGD=∠GAP,
又∵∠CDG=∠AGP,
∴△GCD∽△APG,
∴ ![]() ,
,
∵GF=4,CD=DA=1,AF=x,
∴GD=3﹣x,AG=4﹣x,
∴ ![]() =
= ![]() ,即y=
,即y= ![]() ,
,
∴y关于x的函数关系式为y= ![]() ,
,
当y=3时, ![]() =3,解得x=2.5,
=3,解得x=2.5,
经检验的x=2.5是分式方程的根.
故x的值为2.5
(2)解:∵S1= ![]() GPGD=
GPGD= ![]()
![]() (3﹣x)=
(3﹣x)= ![]() (cm2),
(cm2),
S2= ![]() GDCD=
GDCD= ![]() (3﹣x)×1=
(3﹣x)×1= ![]() (cm2),
(cm2),
∴S1﹣S2= ![]() ﹣
﹣ ![]() =
= ![]() (cm2),即为常数
(cm2),即为常数
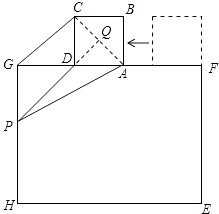
(3)解:延长PD交AC于点Q.
∵正方形ABCD中,AC为对角线,
∴∠CAD=45°,
∵PQ⊥AC,
∴∠ADQ=45°,
∴∠GDP=∠ADQ=45°.
∴△DGP是等腰直角三角形,则GD=GP,
∴3﹣x= ![]() ,
,
化简得:x2﹣5x+5=0.
解得:x= ![]() ,
,
∵0≤x≤2.5,
∴x= ![]() ,
,
在Rt△DGP中,PD= ![]() =
= ![]() (3﹣x)=
(3﹣x)= ![]() (cm)
(cm)
【解析】(1)根据题意表示出AG、GD的长度,再由△GCD∽△APG,利用对应边成比例可解出x的值.(2)利用(1)得出的y与x的关系式表示出S1、S
【考点精析】根据题目的已知条件,利用等腰直角三角形和矩形的性质的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;矩形的四个角都是直角,矩形的对角线相等.

【题目】初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:
打字数/个 | 50 | 51 | 59 | 62 | 64 | 66 | 69 |
人数 | 1 | 2 | 8 | 11 | 5 |
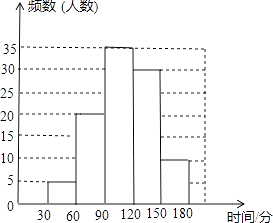
将这些数据按组距5(个字)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次打字成绩的众数是个,平均数是个.