题目内容
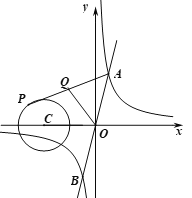
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图像交于A、B两点,点P在以
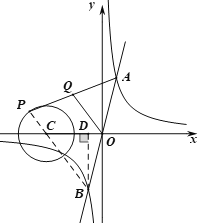
的图像交于A、B两点,点P在以![]() 为圆心,1为半径的⊙C上,Q是AP的中点,则OQ的最大值为( )
为圆心,1为半径的⊙C上,Q是AP的中点,则OQ的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
先联立两个函数解析式求出点A、B的坐标,连接BP,根据三角形的中位线定理可得![]() ,所以当BP最大时,OQ最大,此时BP过圆心C,如图,过点B作BD⊥x轴于点D,在直角△BCD中,根据勾股定理可求得BC的长,即得BP的长,进而可得答案.
,所以当BP最大时,OQ最大,此时BP过圆心C,如图,过点B作BD⊥x轴于点D,在直角△BCD中,根据勾股定理可求得BC的长,即得BP的长,进而可得答案.
解:解方程组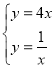 ,得
,得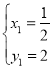 ,
,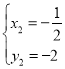 ,∴A(
,∴A(![]() ,2),B(
,2),B(![]() ,-2).
,-2).
连接BP,∵OA=OB,QA=QP,∴![]() ,所以当BP最大时,OQ最大,此时BP过圆心C,如图,过点B作BD⊥x轴于点D,则OD=
,所以当BP最大时,OQ最大,此时BP过圆心C,如图,过点B作BD⊥x轴于点D,则OD=![]() ,BD=2,
,BD=2,
∵OC=2,∴CD=![]() ,
,
在直角△BCD中,根据勾股定理,得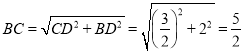 ,
,
∴![]() .
.
∴![]() .
.
故选D.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目