Question

【题目】如图，已知△ABC中，BD平分∠ABC，点M是BD上一点，过M点作EF∥BC，分别交AB、AC于E、F，作MN∥AB交BC于N．

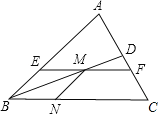
（1）试判断四边形BEMN是什么特殊四边形？并证明你的结论．

（2）连接EN，将△ABC再添加一个什么条件时，四边形EFCN是平行四边形？

Answer 1

【答案】（1）平行四边形BEMN是菱形；（2）BA=BC（条件答案不唯一）．

【解析】

试题分析：因为四边形BEMN的对边都互相平行很容易得到是平行四边形，又因为BD平分∠ABC，所以很容易证得△BEM是等腰三角形所以BE=EM，所以四边形BEMN是菱形；添一个条件：BA=BC即可．

解：（1）四边形BEMN是菱形，

∵EF∥BC，MN∥AB，

∴四边形BEMN是平行四边形，

∵EF∥BC，

∴∠EMB=∠MBN，

又∵∠EBM=∠MBN，

∴∠EMB=∠EBM，

∴EB=EM，

∴平行四边形BEMN是菱形；

（2）条件：BA=BC（条件答案不唯一）．

∵BA=BC，BD平分∠ABC，

∴BD⊥AC，

∵四边形BEMN是菱形，

∴BD⊥EN，

∴AC∥EN，

又∵EF∥CN，

∴四边形EFCN是平行四边形．