题目内容
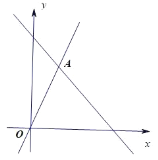
【题目】如图,一次函数 y=-x+6的图像与正比例函数 y=2x 的图像交于点 A.
(1)求点 A 的坐标;
(2)已知点 B 在直线 y=-x+6上,且横坐标为5,在 x 轴上确定点 P,使 PA+PB 的值最小,求出此时 P 点坐标,并直接写出 PA+PB 的最小值.
【答案】(1)点A的坐标(2,4);(2)P 点坐标为(![]() ,0),PA+PB 的最小值为
,0),PA+PB 的最小值为![]() .
.
【解析】
(1)把两个函数关系式联立成方程组求解,即可求得交点A的坐标;
(2)作点B关于![]() 轴的对称点C,连接AC交
轴的对称点C,连接AC交![]() 轴于P,连接PB,此时PA+PB的值最小,利用两点之间的距离公式计算即可求得最小值.
轴于P,连接PB,此时PA+PB的值最小,利用两点之间的距离公式计算即可求得最小值.
(1)解方程组![]() ,
,
得:![]() ,
,
∴点A的坐标为(2,4);
(2) ∵点B在直线![]() 上,且横坐标为5,
上,且横坐标为5,
∴点B的坐标为(5,1),
作B点关于x轴对称点C,
则点C的坐标为(5,-1),
连接AC交![]() 轴于P,连接PB,此时PA+PB的值最小,
轴于P,连接PB,此时PA+PB的值最小,
设直线AC的表达式为![]() ,
,
将点A、C的坐标(2,4)、(5,-1)代入,得:![]() ,
,
解得: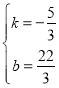 ,
,
∴直线AC的表达式为![]() ,
,
令![]() ,则
,则![]() ,
,
∴P点坐标为(![]() ,0),
,0),
∴PA+PB的最小值=AC=![]() .
.

【题目】甲、乙两名队员参加射击训练(各射击10次),成绩分别被制成下列两个统计图:
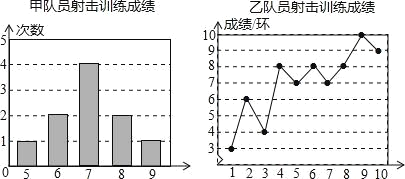
根据以上信息,整理分析数据如下表:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | c | d |
(1)填空:a= ,b= ,c= ,求出 d 的值;
(2)若选派其中一名参赛,你认为应选哪名队员?请说明理由.
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.