��Ŀ����
����Ŀ��������ĸ�ľ����β�����������������ݶ����ӣ����ܹ���һ��ƽ��ͼ�Σ� 
��1�����̶�����ľ��AB��BC��AD������AB=AD=2cm��BC=5cm����ͼ�����õ��ĸ�ľ��CD=5cm���жϴ�ʱ��B���D�Ƿ���ȣ���˵�����ɣ�
��2�����̶�һ��ľ��AB������AB=2cm������ľ��CD=5cm�����ľ��AD��BC�ij��Ȳ��䣬����D�Ƶ�BA���ӳ�����ʱ����CҲ��BA���ӳ����ϣ�����C�Ƶ�AB���ӳ�����ʱ����A��C��D�ܹ����ܳ�Ϊ30cm�������Σ����ľ��AD��BC�ij��ȣ�
���𰸡�
��1���⣺��ȣ�
���ɣ�����AC��
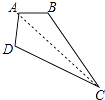
�ڡ�ACD�͡�ACB�У�
�� 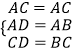 ��
��
���ACD�ա�ACB��SSS����
���B=��D
��2���⣺��AD=x��BC=y��
�ߵ���C�ڵ�D�Ҳ�ʱ�� ![]() �����
����� ![]() ��
��
����C�ڵ�D���ʱ�� ![]() �����
����� ![]() ��
��
��ʱAC=17��CD=5��AD=8��5+8��17��
������⣬
��AD=13cm��BC=10cm��
����������1������AC������SSS֤������������ȫ�ȼ��ɣ���2�����������ٵ���C�ڵ�D�Ҳ�ʱ���ڵ���C�ڵ�D���ʱ���ֱ��г������鼴�ɽ�����⣬ע������������������߹�ϵ�����������Ƿ�������⣮

��ϰ��ϵ�д�
 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
�����Ŀ



