题目内容
【题目】如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足条件时,四边形EFGH是菱形. 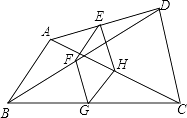
【答案】AB=CD
【解析】解:需添加条件AB=CD. ∵E,F是AD,DB中点,
∴EF∥AB,EF= ![]() AB,
AB,
∵H,G是AC,BC中点,
∴HG∥AB,HG= ![]() AB,
AB,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形,
∵E,H是AD,AC中点,
∴EH= ![]() CD,
CD,
∵AB=CD,
∴EF=EH,
∴四边形EFGH是菱形.
所以答案是:AB=CD.
【考点精析】认真审题,首先需要了解三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半),还要掌握菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形)的相关知识才是答题的关键.

练习册系列答案
相关题目


