题目内容
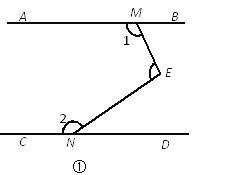
【题目】已知：如图，在长方形
中，AB=4cm，BC=6cm，点
为
中点，如果点
在线段
上以每秒2cm的速度由点
向点
运动，同时，点
在线段
上由点向点
运动．设点运动时间为
秒，若某一时刻△BPE与△CQP全等，求此时的值及点的运动速度．
【答案】见解析
【解析】
由∠B=∠C=90°，可知存在以下两种情况使△BPE≌△CQP，（1）当BP=CP，BE=CQ时；（2）当BP=CQ，BE=CP时；设点Q的运动的时间为vcm/s，则由已知易得BP=2t，CP=6-2t，BE=2，CQ=vt，由此根据上述两种情况分别列出关于t和v的方程，解方程即可求得对应的t和v的值.
设点 
的运动速度为v cm/s，则 
，
，
，
．
∵∠B=∠C=90°，
∴存在以下两种情况使△BPE≌△CPQ.
（1）当BP=CP，BE=CQ时，△BPE≌△CPQ，此时有：
，
，
解得：
，
；
（2）当当BP=CQ，BE=CP时，△BPE≌△CPQ，
此时有：
，
．
解得：
，
．
综上所述，
的值为 
秒，点的速度为
；或的值为
秒，点的速度为2 cm/s．
练习册系列答案
单元期中期末卷系列答案
相关题目
